If f(x) is defined as
f(x)={2x+3x≤03x+3x≥0
then evaluate : limx→0f(x)andlimx→1f(x)
To evaluate the limits limx→0f(x) and limx→1f(x) for the piecewise function defined as:
f(x)={2x+3if x≤03x+3if x>0
we will calculate each limit step by step.
Step 1: Evaluate limx→0f(x)
Left-hand limit:
1. Since we are approaching 0 from the left (x→0−), we use the first case of the function: f(x)=2x+3.
2. Calculate the limit:
limx→0−f(x)=limx→0−(2x+3)=2(0)+3=3
Right-hand limit:
3. Now, we approach 0 from the right (x→0+), we use the second case of the function: f(x)=3x+3.
4. Calculate the limit:
limx→0+f(x)=limx→0+(3x+3)=3(0)+3=3
Conclusion for limx→0f(x):
5. Since both the left-hand limit and right-hand limit are equal:
limx→0f(x)=3
Step 2: Evaluate limx→1f(x)
Left-hand limit:
1. As we approach 1 from the left (x→1−), we use the second case of the function since 1>0: f(x)=3x+3.
2. Calculate the limit:
limx→1−f(x)=limx→1−(3x+3)=3(1)+3=6
Right-hand limit:
3. Now, we approach 1 from the right (x→1+), we still use the second case of the function: f(x)=3x+3.
4. Calculate the limit:
limx→1+f(x)=limx→1+(3x+3)=3(1)+3=6
Conclusion for limx→1f(x):
5. Since both the left-hand limit and right-hand limit are equal:
limx→1f(x)=6
Final Results:
- limx→0f(x)=3
- limx→1f(x)=6
2. Calculate the limit:
limx→0−f(x)=limx→0−(2x+3)=2(0)+3=3
4. Calculate the limit:
limx→0+f(x)=limx→0+(3x+3)=3(0)+3=3
limx→0f(x)=3
2. Calculate the limit:
limx→1−f(x)=limx→1−(3x+3)=3(1)+3=6
4. Calculate the limit:
limx→1+f(x)=limx→1+(3x+3)=3(1)+3=6
limx→1f(x)=6
- limx→1f(x)=6
Topper's Solved these Questions
- LIMITS AND DERIVATIVESBook:NAGEEN PRAKASHAN ENGLISHChapter:LIMITS AND DERIVATIVESExercise:EX-13B
Explore 11 Videos
- LIMITS AND DERIVATIVESBook:NAGEEN PRAKASHAN ENGLISHChapter:LIMITS AND DERIVATIVESExercise:EX-13C
Explore 11 Videos
- LIMITS AND DERIVATIVESBook:NAGEEN PRAKASHAN ENGLISHChapter:LIMITS AND DERIVATIVESExercise:Miscellaneous Exercise
Explore 30 Videos
- INTRODUCTION OF THREE DIMENSIONAL GEOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:INTRODUCTION OF THREE DIMENSIONAL GEOMETRYExercise:Miscellaneous Exercise
Explore 6 Videos
- LINEAR INEQUALITIESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINEAR INEQUALITIESExercise:MISCELLANEOUS EXERCISE
Explore 14 Videos
Similar Questions
Evaluate: limx→0xx
View SolutionEvaluate limx→0f(x), where
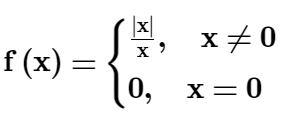
View Solutionlimx→0xsecx
View SolutionIf f(x) is defined as
f(x)=⎧⎪⎨⎪⎩x0≤x≤11x=12−xx>1
then show that limX→1f(x)=1
View SolutionThe value of limx→0|x|x, is
View SolutionEvaluate: limx→0sin5xtan3x.
View SolutionEvaluate : limx→0(1−x)n−1x
View SolutionIf f(x) is defined as
f(x)=⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩x0≤x<120x=121−x12<x≤1
then evaluate : limx→12f(x)
View SolutionEvaluate: limx→0tanx−sinxx3
View SolutionIf f(x) is defined as follows:
f(x)=⎧⎪⎨⎪⎩1x>0−1x<00x=0
Then show that limx→0f(x) does not exist.
View Solution

