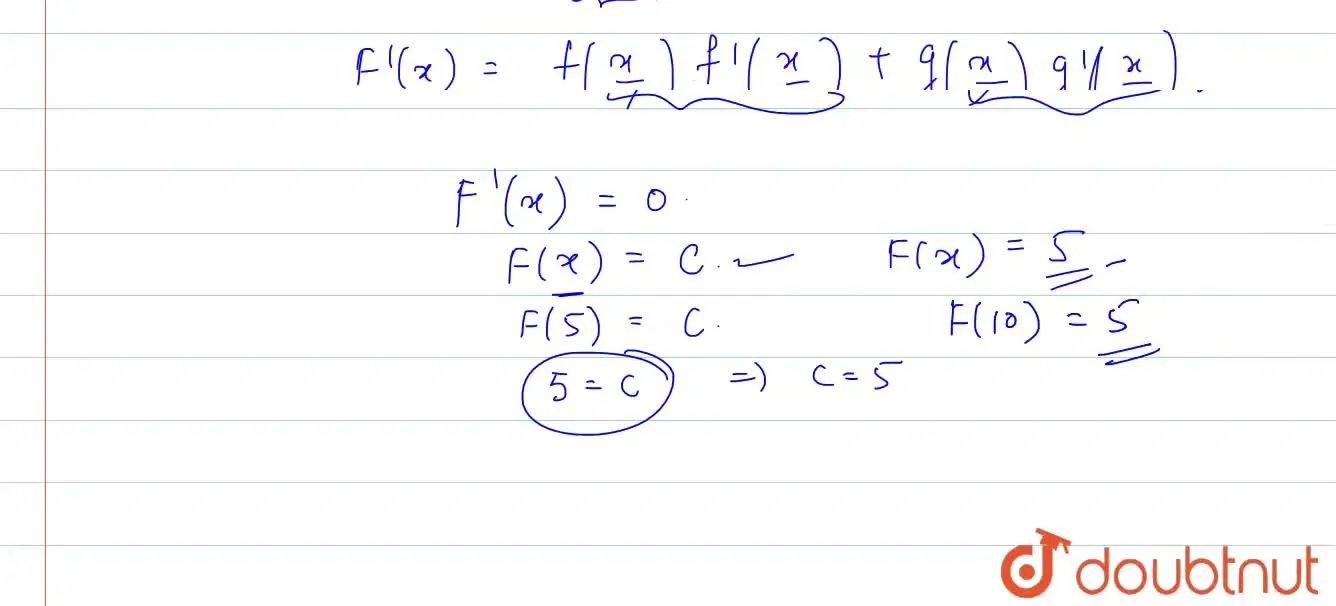If f''(x) =- f(x) and g(x) = f'(x) and F(x)=(f(x2))2+(g(x2))2
and given that F(5) =5, then F(10) is
5
10
0
15
F'(x)=[f(x2)f'(x2)+g(x2)g'(x2)]
Here, g(x)=f'(x)
and g'(x)=f'''(x)=−f(x)
So,F'(x)=f(x2)g(x2)−f(x2)g(x2)=0
Hence, F(x) is a constant function.
Therefore, F(10) =5.
Related Playlists
- BOOK - CENGAGECHAPTER - DIFFERENTIATIONEXERCISE - Exercise (Multiple)22videos
DIFFERENTIATION
- BOOK - CENGAGECHAPTER - DIFFERENTIATIONEXERCISE - Exercise (Comprehension)23videos
DIFFERENTIATION
- BOOK - CENGAGECHAPTER - DIFFERENTIATIONEXERCISE - Exercise 3.914videos
DIFFERENTIATION
- BOOK - CENGAGECHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Question Bank25videos
DIFFERENTIAL EQUATIONS
- BOOK - CENGAGECHAPTER - DOT PRODUCTEXERCISE - DPP 2.115videos
DOT PRODUCT
Similar Questions
If f'(x)=g(x) and g'(x)=−f(x) for all x and f(2)=4=f'(2) then (f(24))2+(g(24))2 is
View SolutionIf f(x)=|x−2| and g(x)=f(f(x)) then g'(x)=
View SolutionIf f(x)=x2andg(x)=x2+1 then: (f∘g)(x)=(g∘f)(x)=
View SolutionIf f(x) is a function such that f(x)+f'(x)=0andg(x)=(f(x))2+(f'(x))2andg(3)=8, rhen g(8)=
View SolutionLet F(x)=(f(x2))2+(g(x2))2.F(5)=5 and f''(x)=−f(x),g(x)=f'(x), then F(10) is equal to:
View SolutionIf f is twice differentiable function such that
f''(x)=−f(x), and f'(x)=g(x),h(x)=[f(x)]2+[g(x)]2 amd h(5)=11, then h(10)=View SolutionIf f(x)=1+2xandg(x)=x2 , then: (f∘g)(x)−(g∘f)(x)=
View SolutionIf f'(x)=g(x) and g'(x)=−f(x) for all x and f(2)=4=f'(2) then f2(4)+g2(4) is
View SolutionLet F(x)=(f(x2))2+(g(x2))2.F(5)=5 and f''(x)=−f(x),g(x)=f'(x), then F(10) is equal to:
View SolutionIf f'(x)=g(x)andg'(x)=−f(x) forall xandf(3)=5=f'(3)then f(2)(119)+g(2)(119)=
View Solution