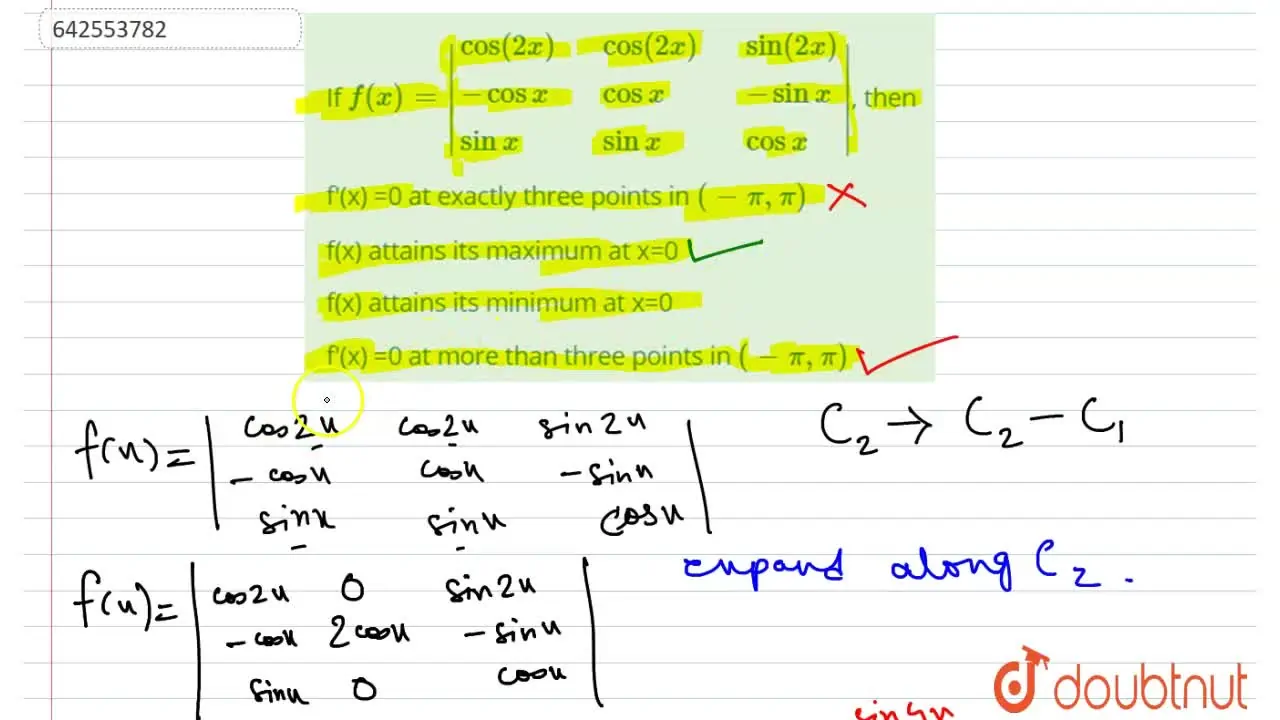
If f(x)=∣∣ ∣ ∣∣cos(2x)cos(2x)sin(2x)−cosxcosx−sinxsinxsinxcosx∣∣ ∣ ∣∣, then
f'(x) =0 at exactly three points in (−π,π)
f(x) attains its maximum at x=0
f(x) attains its minimum at x=0
f'(x) =0 at more than three points in (−π,π)
The correct Answer is:2,4
f(x)=∣(cos(2x),cos(2x),sin(2x).(−cosx,cosx,−sinx),(sinx,sinx,cosx)|}
Now f(X) = -2 sin 2x-4 sin4x=0
→2sin2x(1+4cos2x)=0
→sin2x=0orcos2x=14
for cos 2x=−14 there are four solution
f(x)=0 has more than three solution
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Numerical Value Type24videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Single Correct Answer Type13videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise93videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
Similar Questions
1+sin2x+cos2xcosx+sinx=2cosx
View SolutionIf f(x)=beg∈{vmatrix}cos2x&cos2x&sin2x\−cosx&cosx&−sinx\sinx&sinx&cosxend{vmatrix} then
View Solutioncos4x+cos3x+cos2xsin4x+sin3x+sin2x=cot3x
View SolutionSolve |cosx−2sin2x−cos3x|=1−2sinx−cos2x.
View Solutionsin3x1+cosx+cos3x1−sinx=
View Solutionsin3x1+cosx+cos3x1−sinx=
View SolutionLet =∣∣ ∣∣cosxsinxcosxcos2xsin2x2cos2xcos3xsin3x3cos3x∣∣ ∣∣ then find the values of f(0) and f'(π/2).
View SolutionProve that : cos4xsin3x−cos2xsinxsin4x.sinx+cos6x.cosx = tan 2x
View SolutionSolve sinx−3sin2x+sin3x=cosx−3cos2x+cos3x.
View SolutionShow that '(1-cos 2x + sin x)/(sin 2x + cos x) = tan x'
View Solution