If Δ1=∣∣
∣∣xsinθcosθ−sinθ−x1cosθ1x∣∣
∣∣
and Δ2=∣∣
∣∣xsin2θcos2θ−sin2θ−x1cos2θ1x∣∣
∣∣,x≠, then for all θ∈(0,π2)
Δ1+Δ2=−2(x3+x−1)
Δ1−Δ2=−2x3
Δ1+Δ2=−2x3
Δ1−Δ2=x(cos2θ−cos4θ)
The correct Answer is:C
Given determinants are
Δ1=∣∣
∣∣xsinθcosθ−sinθ−x1cosθ1x∣∣
∣∣
=−x3+sinθcosθ−sinθcosθ+xcos2θ−x+xsin2θ
=−x3
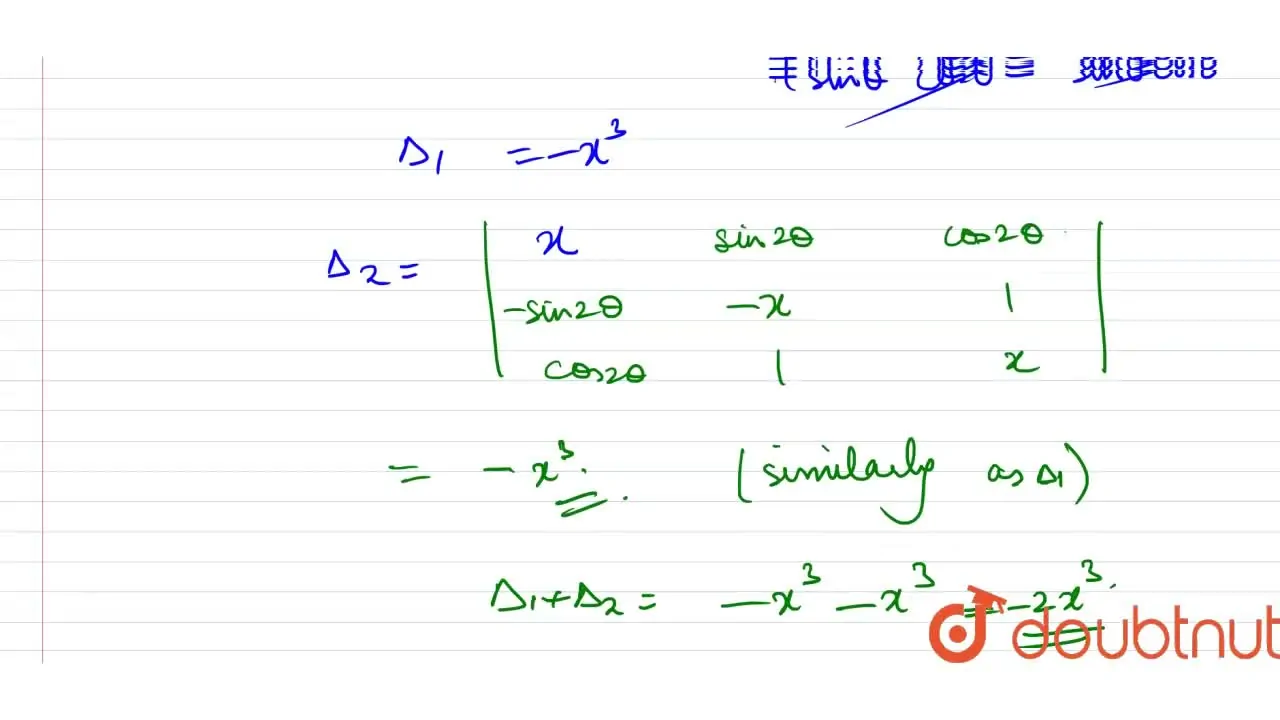
and Δ2=∣∣
∣∣xsin2θcos2θ−sin2θ−x1cos2θ1x∣∣
∣∣,x≠0
=−x3 (similarly as Δ1)
So, according to options, we get Δ1+Δ2=−2x3
Related Playlists
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - MATRICES AND DETERMINANTSEXERCISE - Properties of Determinants (Objective Questions II)4videos
MATRICES AND DETERMINANTS
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - MATRICES AND DETERMINANTSEXERCISE - Properties of Determinants (Numerical Value)1videos
MATRICES AND DETERMINANTS
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - MATRICES AND DETERMINANTSEXERCISE - Types of Matrices, Addition, Substraction, Multiplication and Transposse of a Matrix (Integer Type Question)1videos
MATRICES AND DETERMINANTS
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - LIMIT,CONTINUITY AND DIFFERENTIABILITY EXERCISE - Differentiation (Integer Type Questions)1videos
LIMIT,CONTINUITY AND DIFFERENTIABILITY
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - MISCELLANEOUSEXERCISE - MISCELLANEOUS87videos
MISCELLANEOUS
Similar Questions
If Δ1=∣∣ ∣∣xsinθcosθ−sinθ−x1cosθ1x∣∣ ∣∣ and Δ2=∣∣ ∣∣xsin2θcos2θ−sin2θ−x1cos2θ1x∣∣ ∣∣,x≠0, then for all θ∈(0,π2), Then, Δ1+Δ2=−2xk. The value of k is ________.
View SolutionIf x>0and∣∣ ∣∣xsinθcosθ−sinθx1cosθ1x∣∣ ∣∣=0 then
View SolutionProve that the determinant Δ=∣∣ ∣∣xsinθcosθ−sinθ−x1cosθ1x∣∣ ∣∣ is independent of θ.
View SolutionIf ∣∣ ∣∣xsinθcosθ−sinθ−x1cosθ1x∣∣ ∣∣=8, write the value of x
View SolutionProve that the determinant ∣∣ ∣∣xsinθcosθ−sinθ−x1cosθ1x∣∣ ∣∣ is independent of θ
View SolutionProve that the determinant ∣∣ ∣∣xsinθcosθ−sinθ−x1cosθ1x∣∣ ∣∣ is independent of
View SolutionA value of θ∈(0,π/3), for which
∣∣ ∣ ∣∣1+cos2θsin2θ4cos6θcos2θ1+sin2θ4cos6θcos2θsin2θ1+4cos6θ∣∣ ∣ ∣∣=0, isView Solutionx=asin2θ(1+cos2θ),y=bcos2θ(1−cos2θ) then dydx=
View Solution(sinθ+cosθ)2−1sinθ⋅cosθ
View Solution1+sin2θ+cos2θ1+sin2θ−cos2θ=
View Solution