If cosθ=45 then find the value of (sinθcosθ+tan2θ).
Video Solution
Text Solution
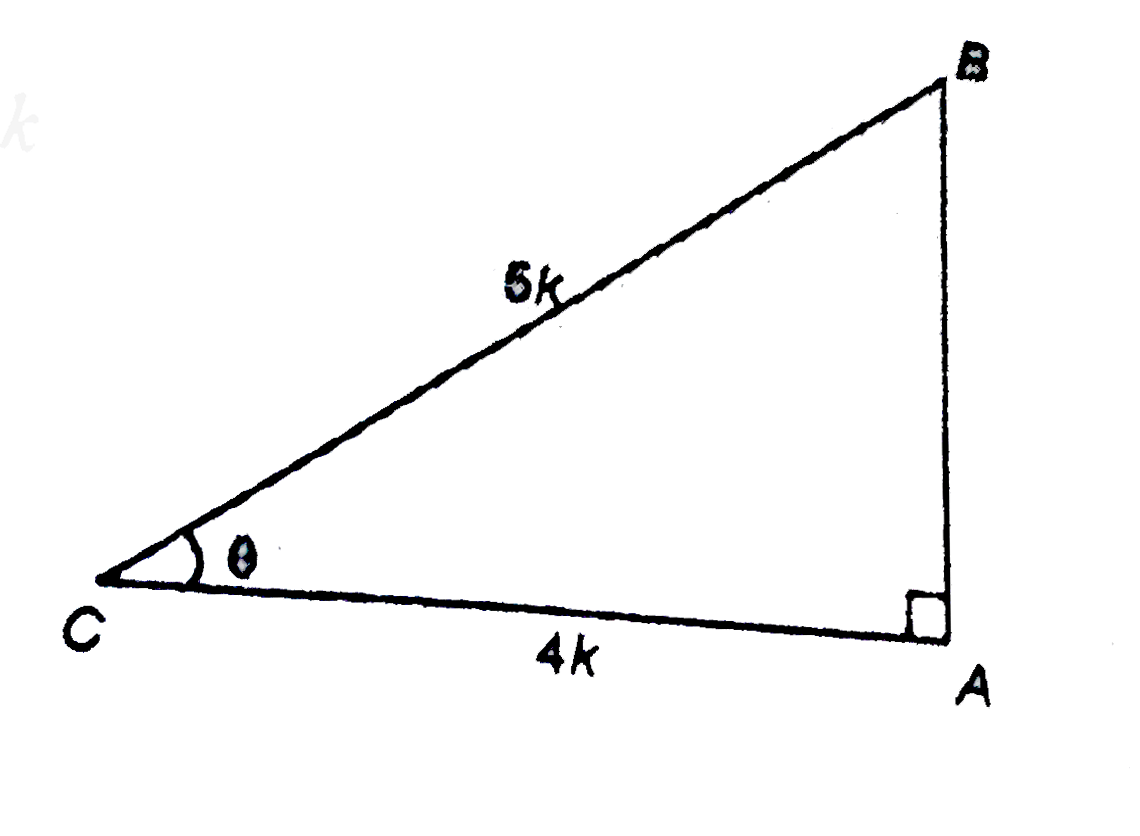
Construct a right - angled ΔABC in which <BAC=90∘,AC=4k
and BC=5k.
In ΔABC,
From Pythagoras theorem
AB2+AC2=BC2
⇒ AB2=BC2−AC2=(5k)2−(4k)2
=25k2−16k2=9k2
⇒ AB=3k
∴ sinθ=ABBC=3k5k=35
and tanθ=ABAC=3k4k=34
Now , sinθcosθ+tan2θ=35⋅45+(34)2=1225+916
192+225400=417400
|
Topper's Solved these Questions
- INTRODUCTION TO TRIGONOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:INTRODUCTION TO TRIGONOMETRYExercise:Problems From NCERT/exemplar
Explore 29 Videos
- INTRODUCTION TO TRIGONOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:INTRODUCTION TO TRIGONOMETRYExercise:Exercise 8a
Explore 20 Videos
- CONSTRUCTIONSBook:NAGEEN PRAKASHAN ENGLISHChapter:CONSTRUCTIONSExercise:Exercise 11 B
Explore 10 Videos
- LINEAR EQUATIONS IN TWO VARIABLES Book:NAGEEN PRAKASHAN ENGLISHChapter:LINEAR EQUATIONS IN TWO VARIABLES Exercise:Revision Exercise Long Answer Questions
Explore 8 Videos
Similar Questions
If cosθ=12,then find the value of 4cos3θ−3cosθ.
View SolutionIf tanθ=43, then find the value of 3sinθ−2cosθ3sinθ+5cosθ
View SolutionIf cosθ=34 , then find the value of 9tan2θ+9 .
View SolutionIf cosθ=1√2,then find the value of cos2θ.
View SolutionIf 3sinθ+4cosθ=5 then find the value of: 4sinθ−3cosθ
View SolutionIf cotθ=125,then find the value ofsinθ⋅secθ+cosθ⋅cosecθ.
View SolutionIf cosθ=513 , find the value of sin2θ−cos2θ2sinθcosθ×1tan2θ
View SolutionIf tanθ=2,then the find the value of 2sinθcosθcos2θ−sin2θ.
View SolutionIf sinθ=1213 , find the value of sin2θ−cos2θ2sinθcosθ×1tan2θ
View SolutionIf cosθ=1√2,then find the value of (tan2θ+1).
View Solution

