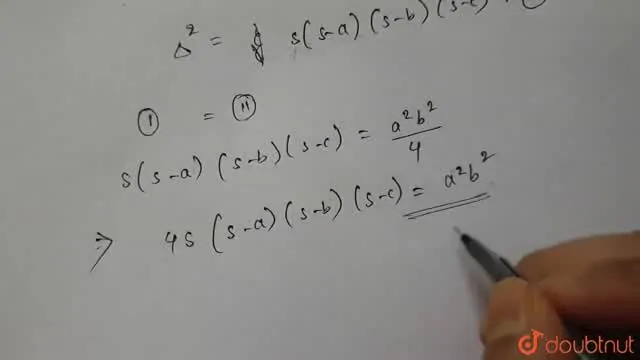If , then prove that
Triangle is right angled at vertex C. Hence,
Area of
Also,
or
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.66videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.74videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.45videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )1videos
PROGRESSION AND SERIES
- BOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)1videos
RELATIONS AND FUNCTIONS
Similar Questions
If c2=a2+b2,2s=a+b+c, then 4s(s−a)(s−b)(s−c)
View SolutionIf c2=a2+b2,2s=a+b+c, then 4Δ2=
View SolutionThe minimum area of the triangle formed by the tangent to x2a2+y2b2=1 and the coordinate axes is (a)ab sq. units (b) a2+b22sq.units (c)(a+b)22sq.units (d) a2+ab+b23 sq. units
View SolutionIn ΔABC,a2(s−a)+b2(s−b)+c2(s−c)=
View SolutionIf S=a+b+c then prove that SS−a+SS−b+SS−c>92 where a,b & c are distinct positive reals.
View SolutionProve that (a+b+c)(b+c−a)(c+a−b)(a+b−c)4b2c2=sin2A
View SolutionElectronic configuration of four elements A, B ,C and D are given below
A) 1s2,2s2,2p6
B) 1s2,2s2,2p4
C) 1s2,2s2,2p6,3s1
D) 1s2,2s2,2p5
Which of the following is the correct order of increasing tendency to gain electron?View SolutionThe electronic structure of four elements A,B,C,D are
(a) 1s2 (b) 1s2,2s2,2p2
( c) 1s2,2s2,2p5 (d) 1s2,2s22p6
The tendency to form electrovalent bond is largest inView SolutionIf A+B+C=2S, prove that : cos2S+cos2(S−A)+cos2(S−B)+cos2(S−C)=2+2cosAcosBcosC.
View SolutionThe electronic configuration for some neutral atoms are given below.
A: 1s22s2, B: 1s22s22p3
C: 1s22s22p4, D: 1s22s22p63s1
In which of this electronic configuration would you expect to have highest (a) IE1 and (b) IE2.View Solution