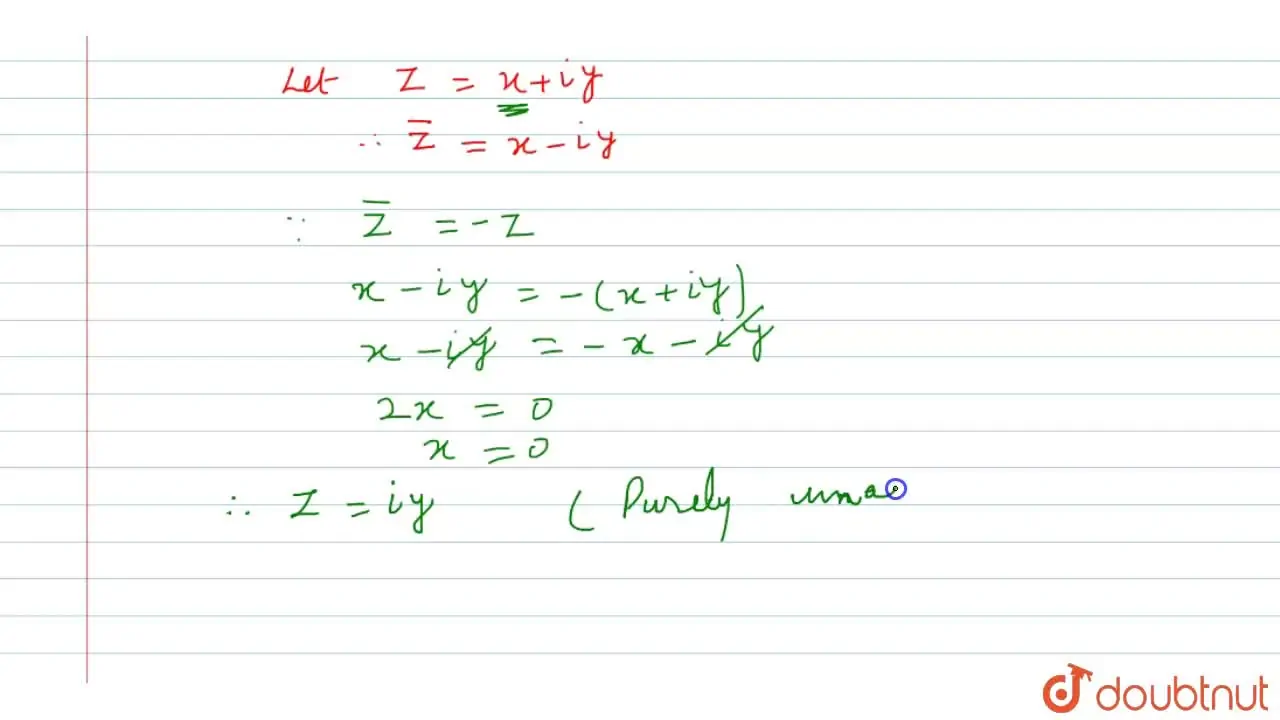If ¯z=−z≠0, show that z is necessarily a purely imaginary number
Step by step video & image solution for If bar(z)= -z ne 0, show that z is necessarily a purely imaginary number by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - ICSECHAPTER - COMPLEX NUMBERSEXERCISE - Exercise (C)21videos
COMPLEX NUMBERS
- BOOK - ICSECHAPTER - COMPLEX NUMBERSEXERCISE - Exercise (D)20videos
COMPLEX NUMBERS
- BOOK - ICSECHAPTER - COMPLEX NUMBERSEXERCISE - Exercise (A)27videos
COMPLEX NUMBERS
- BOOK - ICSECHAPTER - COMPLEX NUMBER EXERCISE - MULTIPLE CHOICE QUESTIONS34videos
COMPLEX NUMBER
- BOOK - ICSECHAPTER - COMPOUND AND MULTIPLE ANGLES EXERCISE - CHEPTER TEST23videos
COMPOUND AND MULTIPLE ANGLES
Similar Questions
If ∣∣∣z|¯z|−¯z∣∣∣=1+|z|, then prove that z is a purely imaginary number.
View SolutionLet z≠i be any complex number such that z−iz+i is a purely imaginary number. Then z+1z is
View SolutionIf |z|=1, then prove that z−1z+1(z≠−1) is a purely imaginary number. What is the conclusion if z=1?
View SolutionIf z1,z2 are complex number such that 2z13z2 is purely imaginary number, then find ∣∣∣z1−z2z1+z2∣∣∣ .
View SolutionIf z1,z2 are complex number such that 2z13z2 is purely imaginary number, then find ∣∣∣z1−z2z1+z2∣∣∣ .
View SolutionIf z is a purely imaginary number then arg (z) may be
View SolutionThe complex number z is purely imaginary , if
View SolutionIf z is a complex number and z=¯z, then prove that z is a purely real number.
View SolutionIf z is a complex number and z=¯z, then prove that z is a purely real number.
View SolutionIf the ratio 1−z1+z is pyrely imaginary, then
View Solution