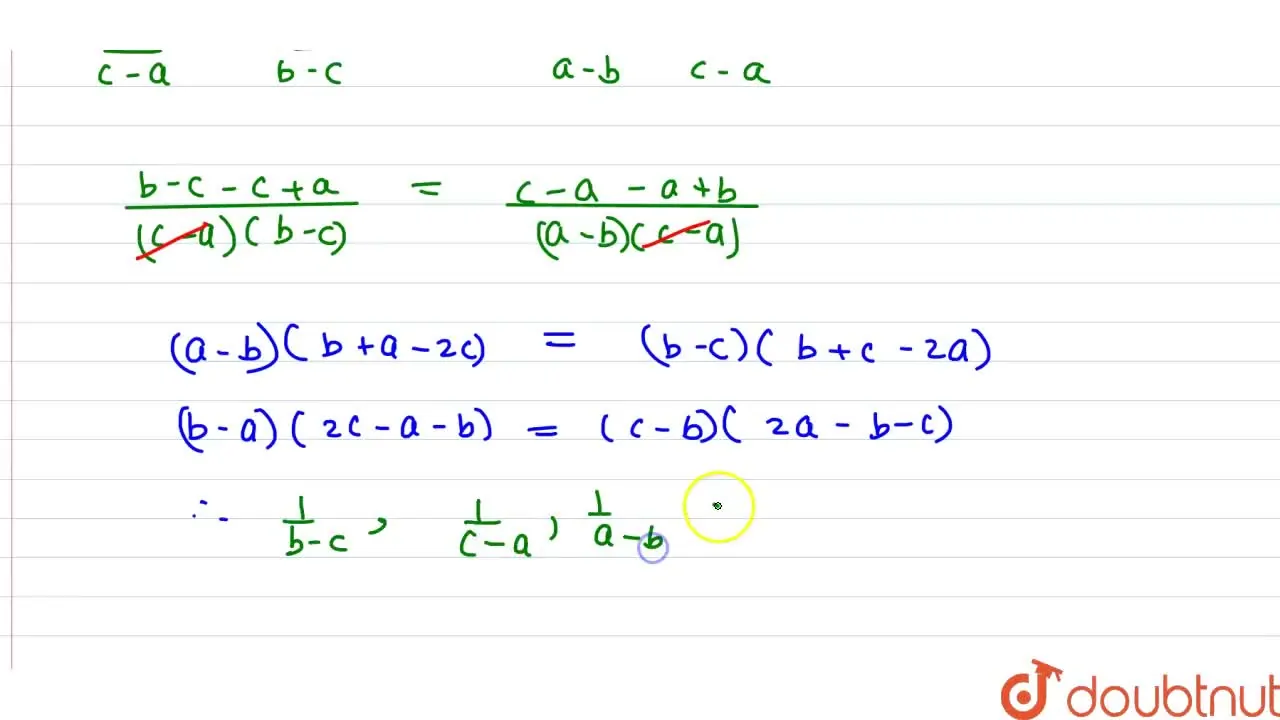if (b−c)2,(c−a)2,(a−b)2 are in AP, prove that
1(b−c),1(c−a),1(a−b) are in AP.
(b−c)2,(c−a)2,(a−b)2 are in AP.
⇒(c−a)2−(b−c)2=(a−b)2−(c−a)2
⇒(b−a)(2c−a−b)=(c−a)(2a−b−c)
Now,1(b−c),1(c−a),1(a−b) will be in AP.
if1(c−a)−1(b−c)=1(a−b)−1(c−a)
i.e if (b−c)−(c−a)(c−a)(b−c)=(c−a)−(a−b)a−b(c−a))
i.e if (a+b−2c)(c−a)(b−c)=(b+c−2a)(a−b)(c−a)
i.e if (a-b) ( a+b -2c) = ( b -c ) ( b+c -2a)
i. e if ( b -a) ( 2c-a-b) = ( c-b) ( 2a -b-c) whichistureby(i)<br>Hence, (b-c)^(2) , ( c-a)^(2) , ( a-b)^(2)are∈AP.<br> Rightarrow 1/((b-c)) , 1/(( c-a)) , 1/((a -b)) are in AP.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Solved Examples16videos
ARITHMETIC PROGRESSION
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Exercise 11A31videos
ARITHMETIC PROGRESSION
- BOOK - RS AGGARWALCHAPTER - APPLICATIONS OF CONIC SECTIONSEXERCISE - EXERCISE 255videos
APPLICATIONS OF CONIC SECTIONS
- BOOK - RS AGGARWALCHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE 10B16videos
BINOMIAL THEOREM
Similar Questions
If (b−c)2,(c−a)2,(a−b)2 are in A.P., then prove that 1b−c,1c−a,1a−b are also in A.P.
View SolutionIf (b−c)2,(c−a)2,(a−b)2 are in A.P., then show that 1b−c,1c−a,1a−b are in A.P.
View SolutionIf (b−c)2,(c−a)2,(a−b)2 are in A.P., then prove that 1b−c,1c−a,1a−b are also in A.P.
View Solutionif (a2+2bc),(b2+2ac),(c2+2ab) are in AP, show that
1 / (( b-c)) ,1/((c -a)) , 1/ ((a-b)) are in AP.View SolutionIf a, b, c are in GP, prove that 1(a+b),12b,1b+c are in AP.
View SolutionIf a2,b2,c2 are in A.P. prove that 1b+c,1c+a,1a+b are in A.P.
View SolutionIf a2,b2,c2 are in A.P., prove that 1b+c,1c+a,1a+b are also in A.P.
View SolutionIf a2,b2,c2 are in AP then prove that 1a+b,1c+b,1a+c are also in AP.
View SolutionIf a2,b2andc2 are in AP then prove that ab+c,bc+aandca+b are also in A.P.
View SolutionIf 1b+c,1c+a,1a+b are in A.P., then
View Solution