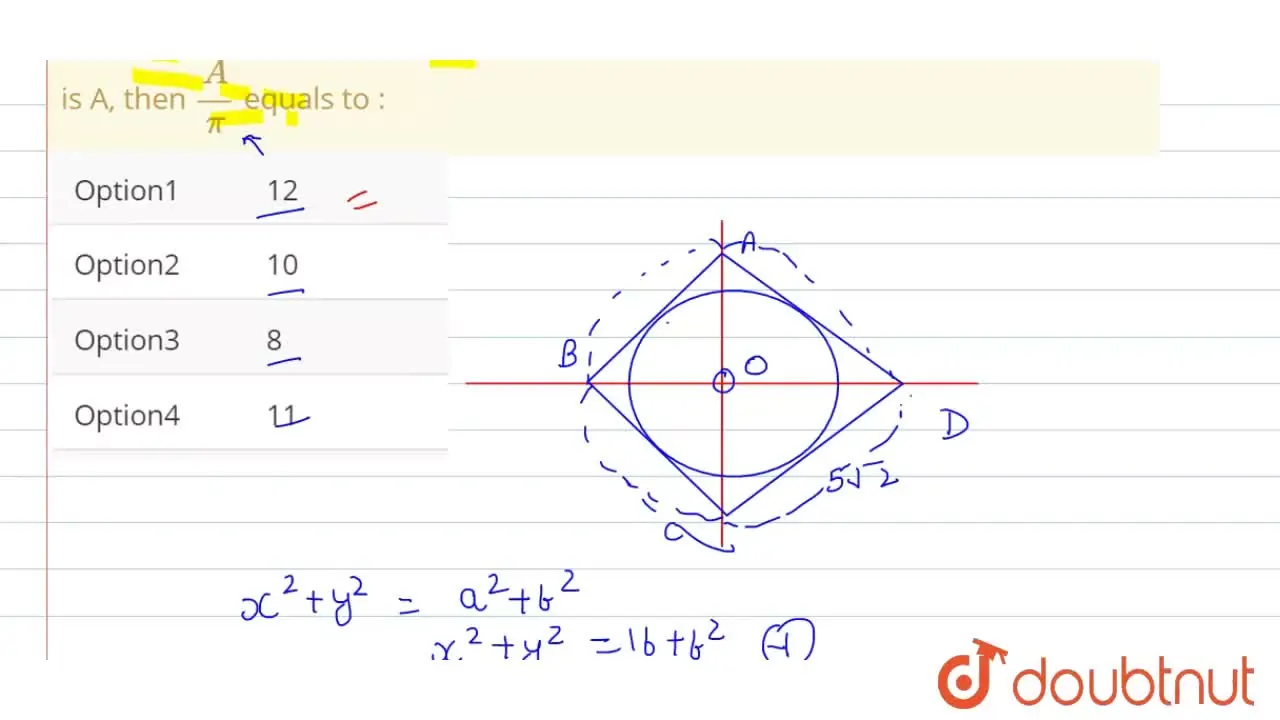
If area of the ellipse $\frac{x^{2}}{16} + \frac{y^{2}}{b^{2}} = 1$ inscribed in a square of side length $5 \sqrt{2}$ is A, then $\frac{A}{π}$ equals to :

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

Answer

Step by step video & image solution for If area of the ellipse (x^(2))/(16)+(y^(2))/(b^(2))=1 inscribed in a square of side length 5sqrt(2) is A, then (A)/(pi) equals to : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK