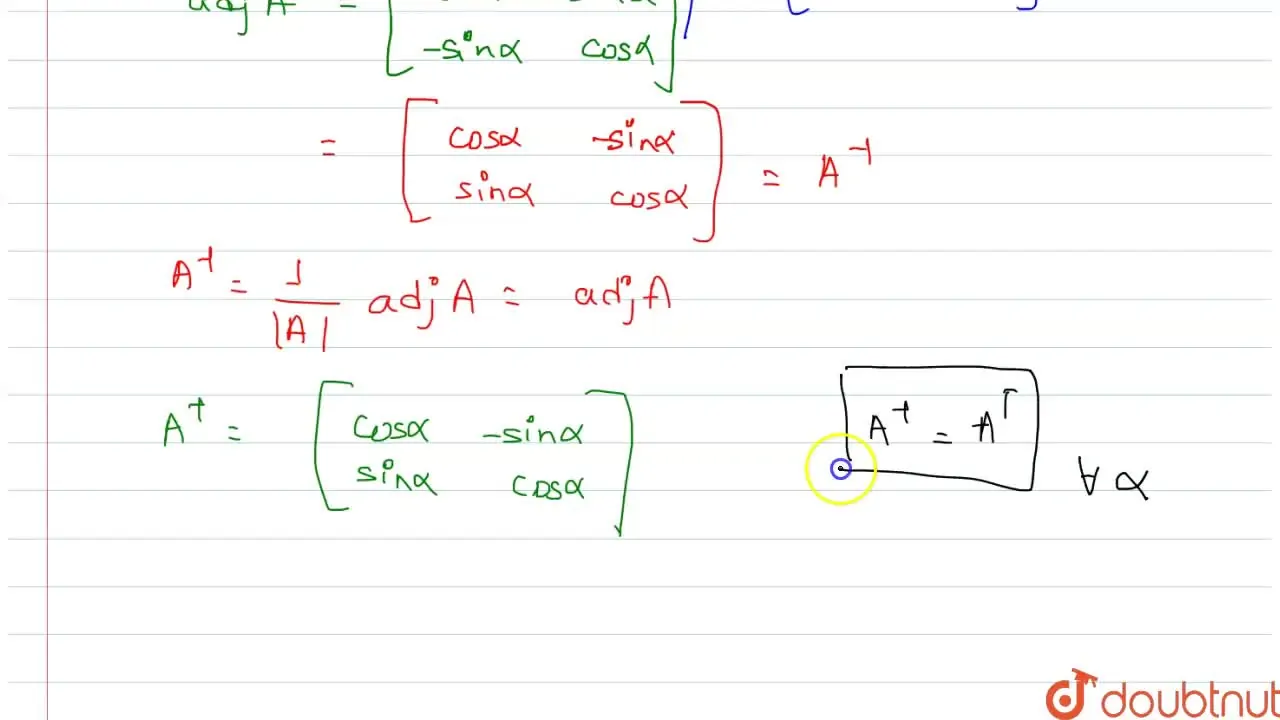
If A=[cosαsinα−sinαcosα] is such that AT=A−1, find α
Step by step video & image solution for If A=[[cosalpha,sinalpha],[-sinalpha,cosalpha]] is such that A^T=A^(-1), find alpha by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
If A=[cosαsinα−sinαcosα] , then verify that AT A=I2 .
View SolutionIf A=[cosαsinα−sinαcosα] then show that A2=[cos2αsin2α−sin2αcos2α]
View SolutionIf A=[cosαsinα−sinαcosα] prove that A.AT=1 Hence find A−1
View SolutionIf A=[cosα−sinαsinαcosα], then A+A′=I, if the value of αis (A) π6 (b) π3 (c) π (d) 3π2
View SolutionIf A=[sinαcosα−cosαsinα], verify that ATA=I2
View SolutionIf Aα=[cosαsinα−sinαcosα] , then prove that AαAβ=Aα+β for every positive integer n .
View SolutionIf (i) A=[cosαsinα−sinαcosα], then verify that A'A=I.(ii) A=[sinαcosα−cosαsinα], then verify that A'A=I.
View SolutionIf A=[cosαsinα−sinαcosα], prove by mathematicasl induction that, An=[cosnαsinnα−sinnαcosnα] for every natural number n
View SolutionIf A=⎡⎢⎣cosα−sinα0sinαcosα0001⎤⎥⎦ , find adj A and verify that A(adj A)=(adj A)A=|A|I3 .
View SolutionLet A=[cosαsinα−sinαcosα] and matrix B is defined such that B=A+3A2+3A3+A4. If |B|=8 then the number of values of α in [0,10π] is
View Solution