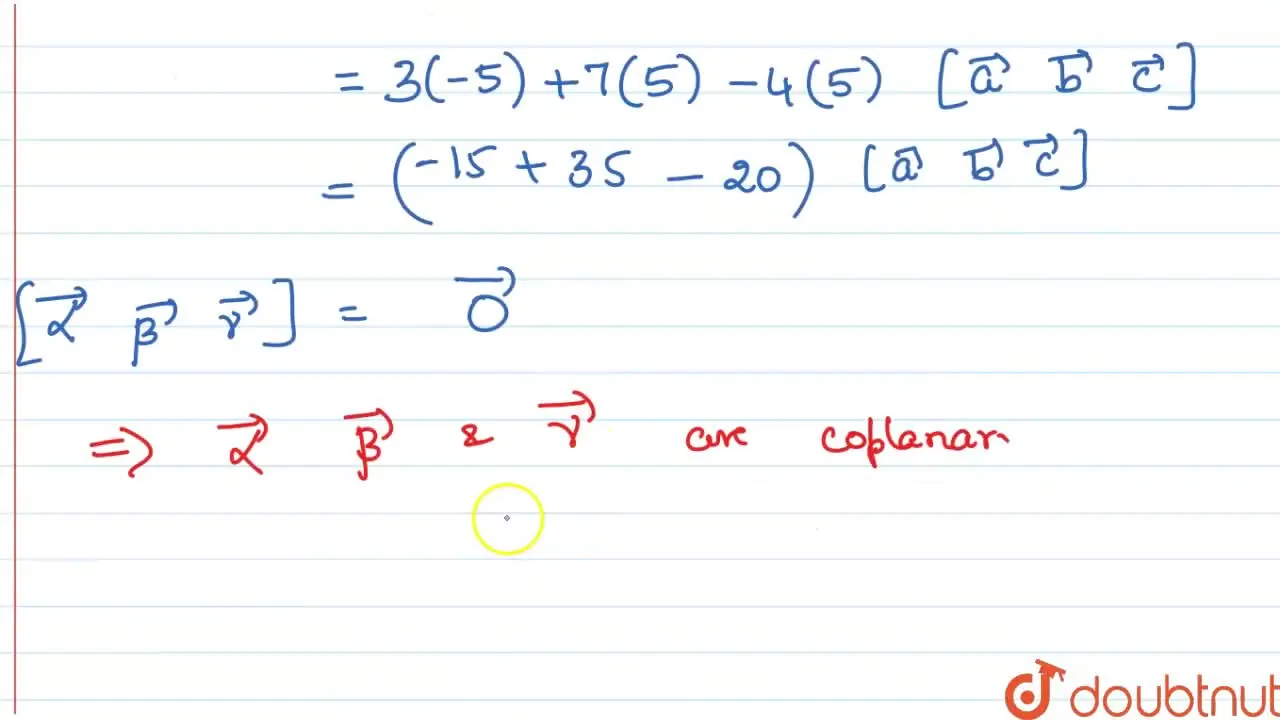If a,b and c are non-coplanar vectors, prove that 3a-7b-4c, 3a-2b+c and a+b+2c are coplanar.Solution in Kannada
Let α=3a−7b−4c,β=3a−2b+c
and γ=a+b+2c
also, let α=xβ,y−γ
⇒3a−7b−4c=x(3a−2b+c)+y(a+b+2c)
=(3x+y)a+(−2x+y)b+(x+2y)c
since, a,b and c are non-coplanar vectors.
therefore, 3x+y=3,−2x+y=−7
and x+2y=−4
solving first two, we find that x=2 and y=-3. these values of x annd y satisfy the third equation as well.
so, x+2 and y=-3 is the unique solution for the above system of equation.
⇒α=2β−3γ
Hence, the vectors α,βandγ are complanar, because α is uniquely written as linear combination of other two.
Trick for the vector α,β,γ to be coplanar, we must have
∣∣
∣∣3−7−43−21112∣∣
∣∣=0, which is true
Hence, α,β,γ are coplanar.
Similar Questions
Show that the points P(a+2b+c),Q(a−b−c),R(3a+b+2c)andS(5a+3b+5c) are coplanar given that a,b and c are non-coplanar.
04:06View SolutionShow that the vectors a−2b+4c,−2a+3b−6cand−b+2c are coplanar vector, where a,b,c are non-coplanar vectors.
02:23View SolutionIf a,b,c are three non-coplanar vectors, then 3a−7b−4c,3a−2b+canda+b+λc will be coplanar, if λ is
03:19View SolutionShow that the points P(a+2b+c),Q(a−b−c),R(3a+b+2c)andS(5a+3b+5c) are coplanar given that a,b and c are non-coplanar.
05:51View SolutionShow that the vectors a−2b+4c,−2a+3b−6cand−b+2c are coplanar vector, where a,b,c are non-coplanar vectors.
04:11View SolutionIf a,b and c are non-coplanar vectors, then prove that the four points 2a+3b−c,a−2b+3c,3a+4b−2canda−6b+6c are coplanar.
06:11View SolutionIf a,b,c are three non-coplanar vectors, then 3a−7b−4c,3a−2b+canda+b+λc will be coplanar, if λ is
03:16View SolutionShow that the vectors a−2b+4c,−2a+3b−6cand−b+2c are coplanar vector, where a,b,c are non-coplanar vectors.
03:36View Solution