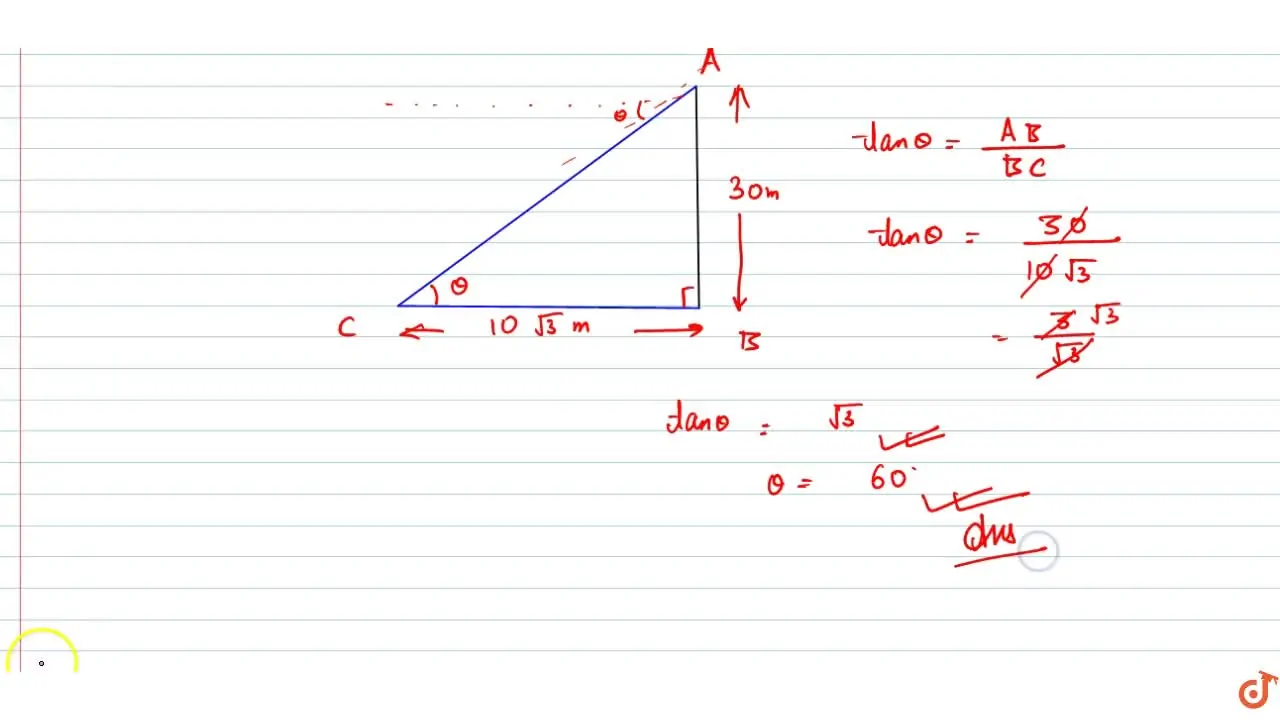
If a tower 30 m high, casts a shadow 10√3m long on the ground, then what is the angle of elevation of the sun ?
Step by step video & image solution for If a tower 30 m high, casts a shadow 10sqrt3 m long on the ground, then what is the angle of elevation of the sun ? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Related Playlists
Similar Questions
If a tower 30 m high, casts a shadow 10√3m long on the ground, then what is the angle of elevation of the sun ?
View SolutionA pole 6 m high casts a shadow 2 3 m long on the ground, then find the angle oi elevation of the sun.
View SolutionIf a pole of 12 m height casts a shadow of 4√3 m long on the ground , then the sun 's angle of elevation at that instant is
View SolutionIf a pole 12 m high casts a shadow 4√3m long on the ground then the sun's elevation is
View SolutionIf a pole of 24m height casts a shdow of 8√3 m long on the ground then the sun's angle of elevation at that instant will be how much?
View SolutionA pole which is 6 m high cast a shadow 2√3 on the ground. What is the sun’s angle of elevation.
View SolutionAn electric pole is 12 m high.If its shadow is 4√3m in length,then what is the angle of elevation of the sun?
View SolutionA pole of height 6 m casts a shadow 2√3 m long on the ground. Find the sun's elevation.
View SolutionIf a flag-staff of 6 m height placed on the top of a tower throws a shadow of 2√3 m along the ground, then what is the angle that the sun makes with the ground?
View SolutionIf a flag-staff of 6 m height plated on the top of a tower throws a shadow of 2√3 m along the ground then what is the angle that the sun makes with the ground ?
View Solution