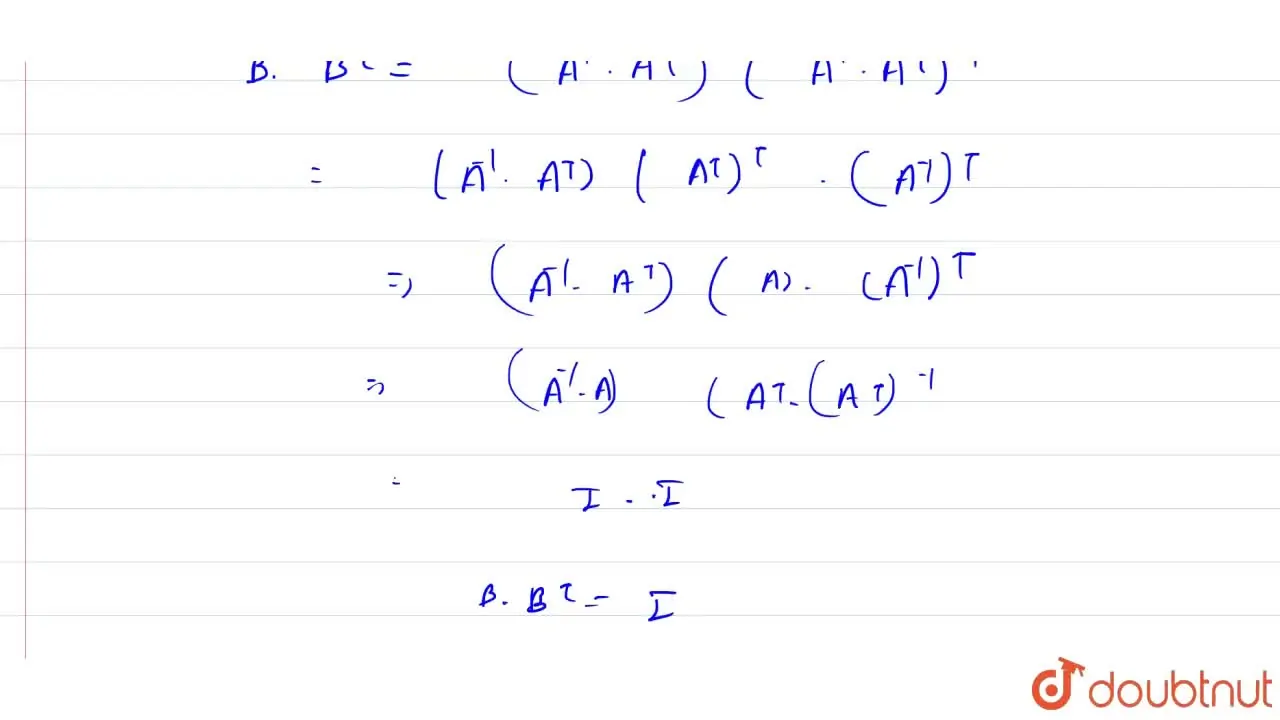If A is an 3×3 non-singular matrix such that AAT=ATAandB=A−1AT, then BBT equals
B−1
(B−1)T
I+B
[2015012015]
The correct Answer is:D
We have,
∴BBT=(A−1AT)(A−1AT)T
=(A−1AT)((AT)T(A−1)T)
=(A−1AT)(A(A−1)T)[∵(AT)T=A]
=A−1(ATA)(A−1)T
=A−1(AAT)(AT)−1[∵ATA=AAT(given)and(A−1)T=(AT)−1]
=(A−1A)(AT(AT)−1)=I=I
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - MATRICESEXERCISE - Section I - Solved Mcqs57videos
MATRICES
- BOOK - OBJECTIVE RD SHARMACHAPTER - MATRICESEXERCISE - Section I - Assertion Reason Type12videos
MATRICES
- BOOK - OBJECTIVE RD SHARMACHAPTER - LOGARITHMSEXERCISE - Chapter Test21videos
LOGARITHMS
- BOOK - OBJECTIVE RD SHARMACHAPTER - MEAN VALUE THEOREMSEXERCISE - Exercise28videos
MEAN VALUE THEOREMS
Similar Questions
If A is an 3×3 non-singular matrix such that AA′=A′A and B=A−1A′ , then BB′equals (1) I+B (2) I (3) B−1 (4) (B−1)′
View SolutionIf A is a 3×3 non-singular matrix such that AAT=ATA and B=A−1AT, then BBT is equal to
View SolutionIf A is a 3×3 non-singular matrix such that AA'=A'A and B=A−1A', then BB' equals:
View SolutionIf A is a 3×3 non-singular matrix such that AA'=A'A and B=A−1A', then BB' equals:
View SolutionIf A is a nonsingular matrix such that AAT=ATA and B=A−1AT, then matrix B is
View SolutionIf A is an 3×3 non-singular matrix such that ∀′=A′A and B=A−1A′ , then BB equals (1) I+B (2) I (3) B−1 (4) (B−1)′
View SolutionIf A is a non-singular matrix such that ∀T=ATA and B=A−1AT, the matrix B is a. involuntary b. orthogonal c. idempotent d. none of these
View SolutionIf A is an 3×3 non-singular matrix such that AA′=A′AandB=A−1A′, then BB' equals: (a)B−1 (b) (B−1)' (c) I+B (d) I
View SolutionIf A is a square matrix such that AAT=I=ATA, then A is
View SolutionIf A is a 3×3 non-singular matrix, then ∣∣A−1adj(A)∣∣ is
View Solution