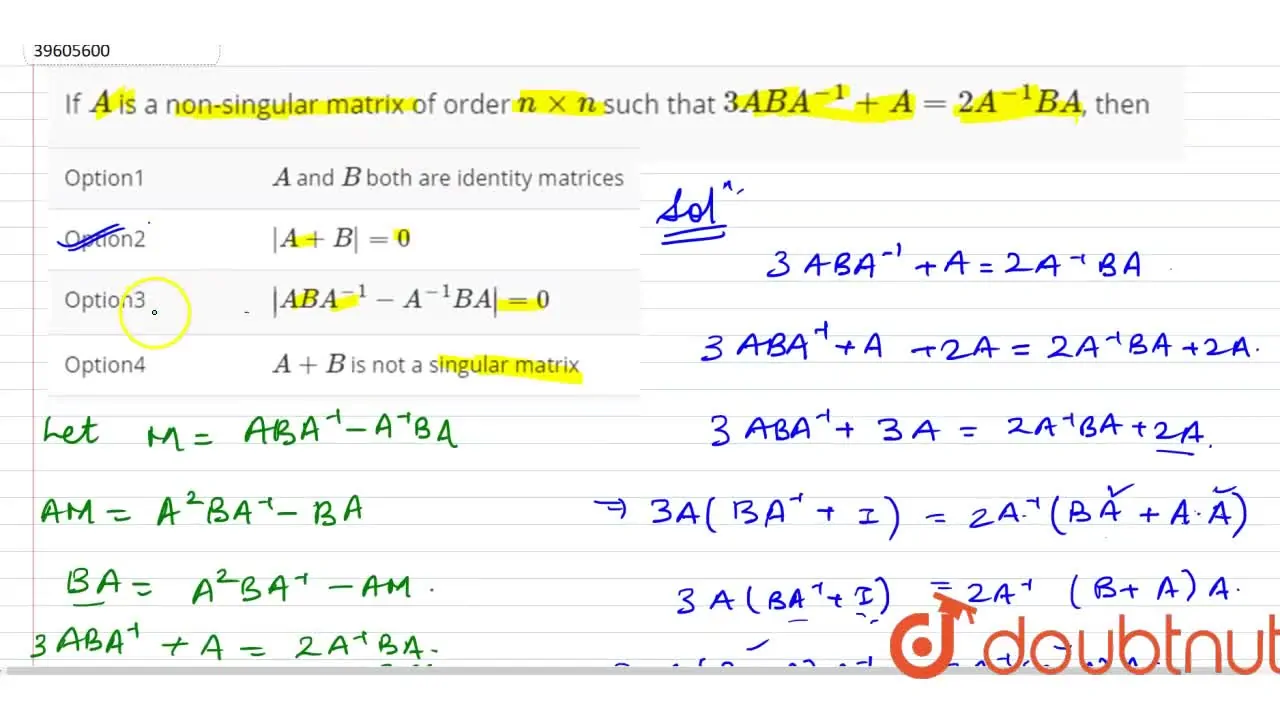
If is a non-singular matrix of order such that , then
A
and both are identity matrices
B
C
D
is not a singular matrix
Video Solution
Text Solution
The correct Answer is:B, C
Let
(as )
or ......
Let
Now
Taking determinants both sides we get
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGECHAPTER - MATRICESEXERCISE - Solved Examples And Exercises165videos
MATRICES
- BOOK - CENGAGECHAPTER - MATRICESEXERCISE - Single correct Answer34videos
MATRICES
- BOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - JEE Previous Year10videos
MATHMETICAL REASONING
- BOOK - CENGAGECHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
Similar Questions
If A is non-singular matrix of order, n×n,
 View Solution
View SolutionIf A is a non-singular matrix, then
View SolutionIf A is a non-singular matrix of order n, then A(adjA)=
View SolutionIf A is a non-singular matrix of order n×n, then : |adj⋅A|=
View SolutionIf A is non-singular matrix of order 3 ,then the rank of A=
View SolutionIf A is a non-singular matrix of order 3, then ∣∣adjA3∣∣=
View SolutionIf A is non singular matrix of order 3, then the rank of A=
View SolutionIf A is a non-singular matrix of order 3, (adjA)+A−1=0, then |A|=
View SolutionGiven that A is a non-singular matrix of order 3 such that A2=2A, then value of |2A| is:
View SolutionIf A is a non singular matrix of order 3 then|adj(A)|=……………
View Solution