If a circle of radius R passes through the origin O and intersects the coordinate axes at A and B, then the locus of the foot of perpendicular from O on AB is
(x2+y2)2=4R2x2y2
(x2+y2)3=4R2x2y2
(x2+y2)(x+y)=R2xy
(x2+y2)2=4Rx2y2
The correct Answer is:B
Let the foot of perpendicular be P(h,k). Then, the slope of line OP=kh
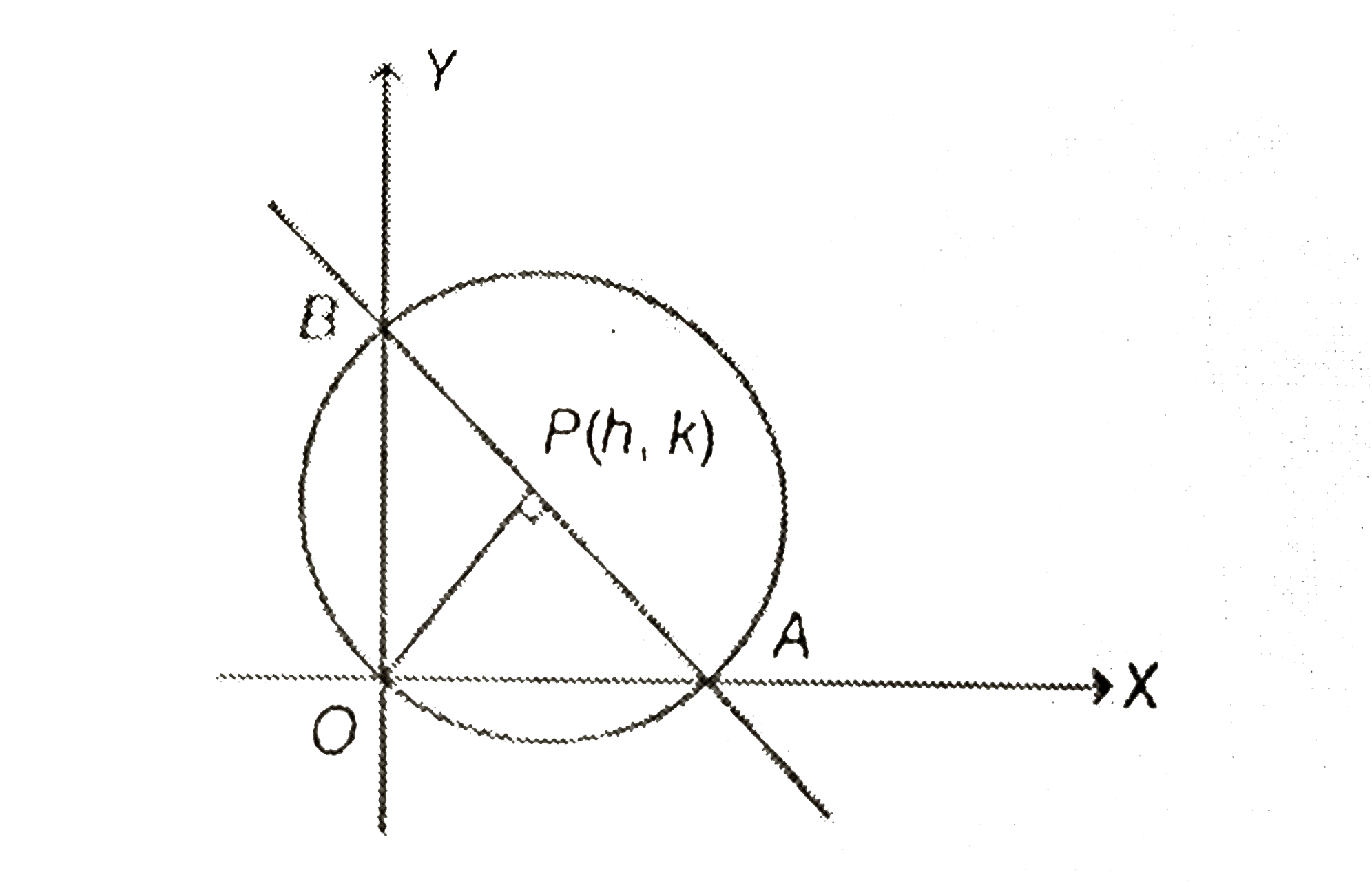
∴ Line AB is perpendicular to line OP, so slope of line AB=−hk [∴ product of slope of two perpendicular line s is (-1)]
Now, the equation of line AB is
y−k=−hk(x−h)⇒hx+ky=h2+k2
or x(h2+k2h)+y(h2+k2k)=1
So, point A(h2+k2h,0)andB(0,h2+k2h)
∴ΔAOB is a right angled triangle, so AB is one of the diameter of the circle having radius R (given).
⇒AB=2R
⇒√(h2+k2k)2+(h2+k2k)=2R
⇒(h2+k2)2(1h2+1k2)=4R2
⇒(h2+k2)=4R2h2k2
On replacing h by x and k by y, we get
(x2+y2)3=4R2x2y2,
which is teh required locus.
Related Playlists
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 1(Objective Question II)2videos
CIRCLE
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 1Fill in the blanks2videos
CIRCLE
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - BINOMIAL THEOREMEXERCISE - Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )8videos
BINOMIAL THEOREM
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - COMPLEX NUMBERSEXERCISE - TOPIC 5 DE-MOIVRES THEOREM,CUBE ROOTS AND nth ROOTS OF UNITY (INTEGER ANSWER TYPE QUESTION)1videos
COMPLEX NUMBERS
Similar Questions
If a circle of radius R passes through the origin O and intersects the coordinates axes at A and B, then the locus of the foot of perpendicular from O on AB is:
View SolutionA circle of constant radius 5 units passes through the origin O and cuts the axes at A and B. Then the locus of the foot of the perpendicular from O to AB is (x2+y2)2(x−1+y−2)=k then k=
View SolutionA circle of constant radius r passes through the origin O and cuts the axes at A and B. Show that the locus of the foot of the perpendicular from O to AB is (x2+y2)2(x−2+y−2)=4r2.
View SolutionA circle of constant radius r passes through the origin O and cuts the axes at A and B. Show that the locus of the foot of the perpendicular from O to AB is (x2+y2)2(x−2+y−2)=4r2.
View SolutionA circle of constant radius r passes through the origin O, and cuts the axes at A and B. The locus of the foots the perpendicular from O to AB is (x2+y2)k=4r2x2y2, Then the value of k is
View SolutionA circle of constant radius r passes through the origin O, and cuts the axes at A and B. The locus of the foots the perpendicular from O to AB is (x2+y2)=4r2x2y2, Then the value of k is
View SolutionA circle of radius r passes through the origin and meets the axes at A and B. The locus of the centroid of △OAB is
View SolutionA circle of radius r passes through the origin O and cuts the axes at AandB. Let P be the foot of the perpendicular from the origin to the line AB. Find the equation of the locus of P.
View SolutionA circle of radius r passes through the origin O and cuts the axes at AandB. Let P be the foot of the perpendicular from the origin to the line AB. Find the equation of the locus of P.
View SolutionA circle of radius 'r' passes through the origin O and cuts the axes at A and B,Locus of the centroid of triangle OAB is
View Solution

