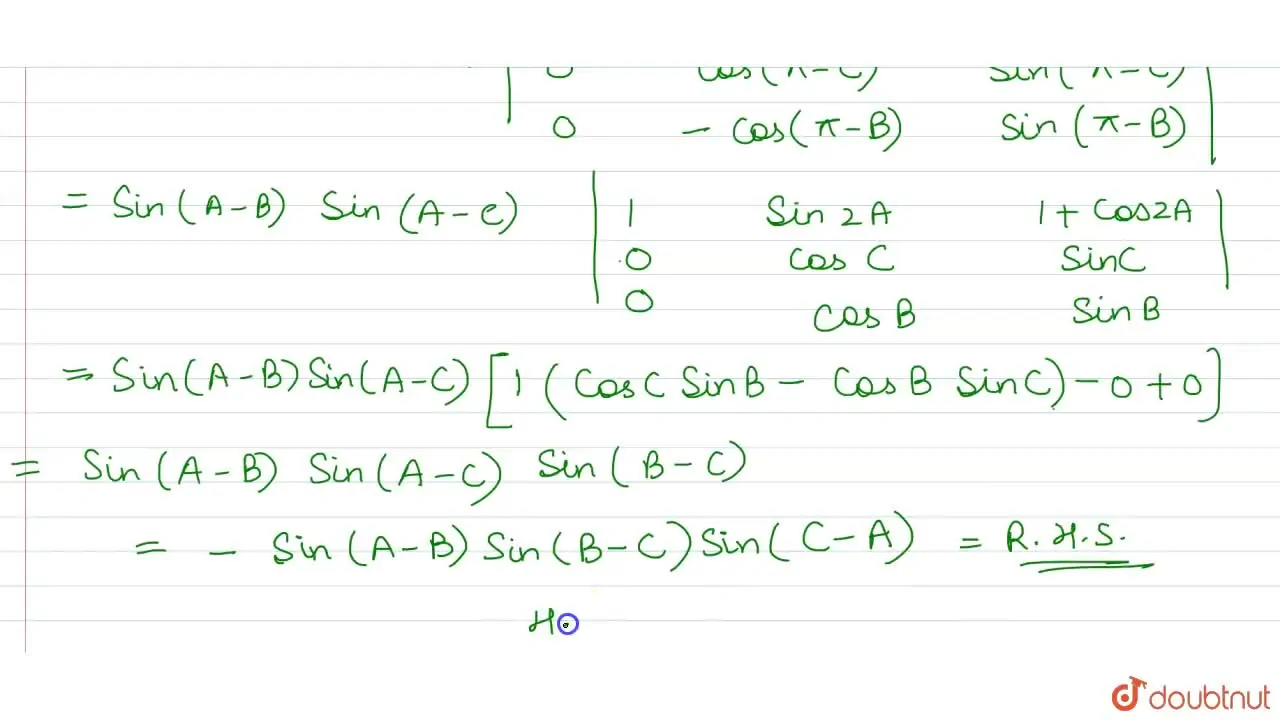If A+B+C =π, show that
∣∣
∣
∣∣sin2Asin A cos Acos2Asin2Bsin B cos Bcos2Bsin2Csin C cos Ccos2C∣∣
∣
∣∣=−sin (A-B)sin(B-C)sin(C-A)
Let the given determinant be Δ. Then,
Δ=∣∣
∣
∣∣1(1/2)sin2A(1/2)(1+cos2A)1(1/2)sin2B(1/2)(1+cos2B)1(1/2)sin2C(1/2)(1+cos2C)∣∣
∣
∣∣[C1→C1+C3]
=14⋅∣∣
∣∣1sin2A1+cos2A0sin2B1+cos2B1sin2C1+cos2C∣∣
∣∣
=14⋅∣∣
∣∣1sin2A1+cos2A0sin2B−sin2Acos2B−cos2A0sin2C−sin2Acos2C−cos2A∣∣
∣∣{R2→R2−R1R3→R3−R1}
=14⋅∣∣
∣
∣∣1sin2A1+cos2A02cos(A+B)sin(B−A)2sin(A+B)sin(A−B)02cos(A+C)sin(C−A)2sin(A+C)sin(A−C)∣∣
∣
∣∣
=sin(A−B)sin(A−C)⋅∣∣
∣
∣∣1sin2A1+cos2A0−cos(A+B)sin(A+B)0−cos(A+C)sin(A+C)∣∣
∣
∣∣[taking 2sin(A-B) common from R2and 2sin (A-C) common fromR3]
=sin(A−B)sin(A−C)⋅∣∣
∣
∣∣1sin2A1+cos2A0−cos(π−C)sin(π−C)0−cos(π−B)sin(π−B)∣∣
∣
∣∣[∵A+B+C=π]
=sin(A−B)sin(A−C)⋅∣∣
∣∣1sin2A1+cos2A0cosCsinC0cosBsinB∣∣
∣∣
=sin(A−B)sin(A−C)[sinBcosC−cos B sin C]
=sin (A-B) sin (A-C) sin (B-C)
=−sin(A-B) sin (B-C) sin (C-A)
Hence, Δ,=−sin (A-B) sin (B-C) sin (C-A)
Related Playlists
- BOOK - RS AGGARWALCHAPTER - DETERMINANTSEXERCISE - Exercise 6A22videos
DETERMINANTS
- BOOK - RS AGGARWALCHAPTER - DETERMINANTSEXERCISE - Exercise 6B44videos
DETERMINANTS
- BOOK - RS AGGARWALCHAPTER - DEFINITE INTEGRALSEXERCISE - Objective Questions73videos
DEFINITE INTEGRALS
- BOOK - RS AGGARWALCHAPTER - DIFFERENTIAL EQUATIONS AND THEIR FORMATION EXERCISE - Exercise 18C16videos
DIFFERENTIAL EQUATIONS AND THEIR FORMATION
Similar Questions
If A+B+C=π, show that ∣∣ ∣ ∣∣sin2AsinAcosAcos2Asin2BsinBcosBcos2Bsin2CsinCcosCcos2C∣∣ ∣ ∣∣=−sin(A−B)sin(B−C)sin(C−A)
View SolutionIf A+B+C=π, prove that sin2A+sin2B−sin2C=4cosAcosBsinC
View SolutionIf A+B+C=180∘, show that sin2A−sin2B−sin2C=−4sinAcosBcosC
View SolutionIf A+B+C=π, prove that
sin2A−sin2B+sin2C=4cosAsinBcosC.View SolutionIf A+B+C=π, prove that sin2A+sin2B+sin2C=2(1+cosAcosBcosC)
View SolutionIf A+B+C=π then prove that Sin2A−Sin2B+Sin2C=4cosAsinBcosC
View SolutionIf A+B+C=180∘, prove that:
sin2A+sin2B+sin2C=2(1+cosAcosBcosC).View SolutionIf A + B + C = π , Prove that sin2A+sin2B−sin2C=2sinAsinBcosC
View SolutionIfA+B+C=π, prove that:
sinA+sinB−sinC=4sinA2sinB2cosC2.View SolutionIf A+B+C=π2 ,prove that:
(i)cos2A+cos2B+cos2C=2+2sinAsinBsinC
(ii)sin2+sin2B+sin2C=1−2sinAsinBsinC.View Solution