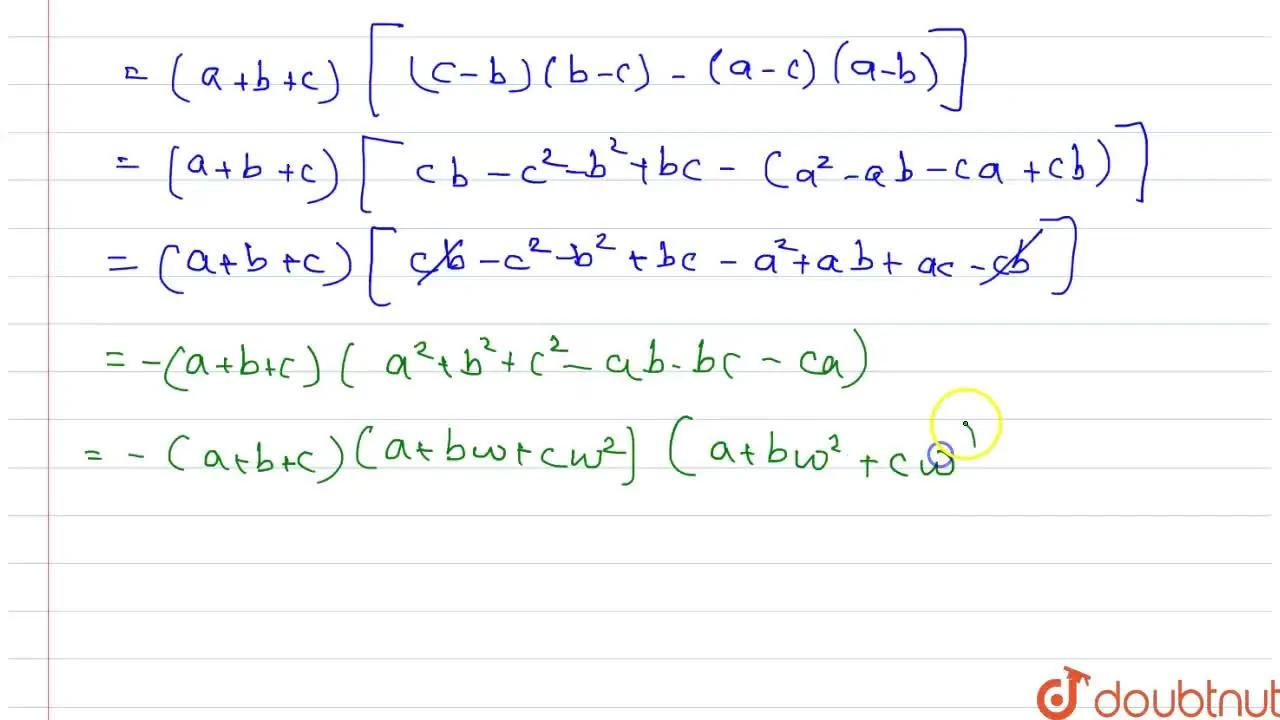If a,b,c are real numbers, prove that ∣∣ ∣∣abcbcacab∣∣ ∣∣=−(a+b+c)(c+bw+cw2)(a+bw2+cw), where w is a complex cube root of unity.
L.H.S.=∣∣
∣∣abcbcacab∣∣
∣∣
Applying C1→C1+C2+C3
=∣∣
∣∣a+b+cbca+b+ccaa+b+cab∣∣
∣∣
=(a+b+c)∣∣
∣∣1bc1ca1ab∣∣
∣∣
Applying R2→R2−R1 and R3→R3−R1
=(a+b+c)∣∣
∣∣1bc0c−ba−c0a−bb−c∣∣
∣∣
=(a+b+c)[1((c−b)(b−c)−(a−b)(a−c))−0+0]
=−(a+b+c)[(b−c)2+a2−ab−ac+bc]
=−(a+b+c)[b2+c2−2bc+a2−ab−ac+bc]
=−(a+b+c)[a2+b2+c2−ab−ac−bc]
Now, (a2+b2+c2−ab−ac−bc)=(a+bω+cω2)(a+bω2+cω)
So, our determinant becomes,
=−(a+b+c)(a+bω+cω2)(a+bω2+cω)
=R.H.S.
Related Playlists
Similar Questions
If a,b,c are real numbers, prove that beg∈{vmatrix}a&b&c\b&c&a\c&a&b\end{vmatrix}=-(a+b+c)(c+b w+c w^2)(a+ bw^2+cw), where \ \ w is a complex cube root of unity.
View SolutionUsing properties of determinant, If f(x)=a+bx+cx2, prove that ∣∣ ∣∣abcbcacab∣∣ ∣∣=−f(1)f(ω)f(ω2),ω is a cube root of unity
View SolutionIf f(x)=a+bx+cx2∀a,b,c∈R and a,b,c are distinct, then value of |abcbcacab| is (where ω&ω2 are complex cube roots of unity) f(1)f(ω)f(ω2) (b) −f(ω)f(ω2) −f(1)f(ω)f(ω2) (d) f(ω)f(ω2)
View SolutionProve that the lines ax+by+c=0,bx+cy+a=0andcx+ay+b=0 are concurrent if a+b+c=0 or a+bω+cω2+cω=0 where ω is a complex cube root of unity .
View SolutionIf a,b,c are positive real numbers such that a+b+c=1, then prove that ab+c+bc+a+ca+b≥32
View SolutionIf a,b,c and u,v,w are the complex numbers representing the vertices of two triangles such that (c=(1−r)a+rb and w=(1−r)u+rv, where r is a complex number, then the two triangles (a)have the same area (b) are similar (c)are congruent (d) None of these
View SolutionProve that [abc][uvw]=∣∣ ∣∣a⋅ub⋅uc⋅ua⋅vb⋅vc⋅va⋅wb⋅wc⋅w∣∣ ∣∣
View Solution1a+ω+1b+ω+1c+ω+1d+ω=1ω where, a,b,c,d, ∈ R and ω is a complex cube root of unity then find the value of ∑1a2−a+1
View SolutionThe complex number associated with the vertices A,B,C of ΔABC are eiθ,ω,¯¯ω, respectively [ where ω,¯¯ω are the com plex cube roots of unity and cosθ>Re(ω)], then the complex number of the point where angle bisector of A meets cumcircle of the triangle, is
View SolutionIf p=a+bω+cω2, q=b+cω+aω2, and r=c+aω+bω2, where a,b,c≠0 and ω is the complex cube root of unity, then (a) p+q+r=a+b+c (b) p2+z2+r2=a2+b2+c2 (c) p2+z2+r2=−2(pq+qr+rp) (d) none of these
View Solution