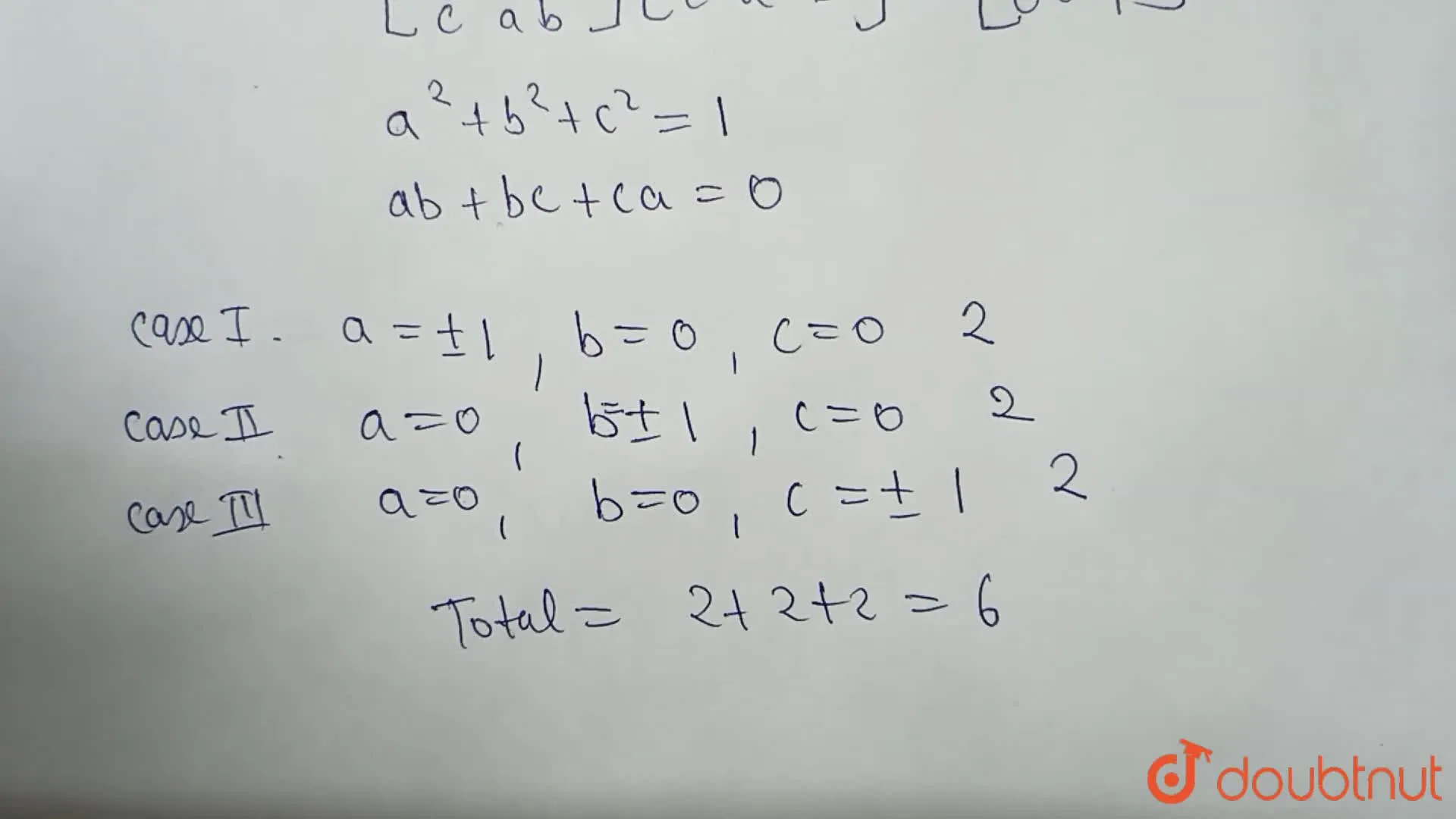If a, b, and c are integers, then number of matrices A=⎡⎢⎣abcbcacab⎤⎥⎦ which are possible such that AAT=I is _______.
The correct Answer is:6
AAT=I
∴A2+b2+c2=1 and ab+bc+ca=0
This is possible when
(i) a=±1,b=c=0
(ii) a=0,b=±1,c=0
(iii) a=0,b=0,c=±1
So, there are six such matrices A.
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - Archives (Single correct Answer type)11videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - JEE Advanced (Single Correct Answer Type)5videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - Matrix Type5videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATHMETICAL REASONINGEXERCISE - Archives10videos
MATHMETICAL REASONING
- BOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
Similar Questions
If a, b and c are consecutive integers, what is a+b+c?
View SolutionThe value of ∣∣ ∣∣a−bb+cab−ac+abc−aa+bc∣∣ ∣∣ is
View SolutionIf a, b and c are distinct positive numbers, then the expression (a+b−c)(b+c−a)(c+a−b)−abc is:
View SolutionIf a, b and c are distinct positive numbers, then the expression (a+b−c)(b+c−a)(c+a−b)−abc is:
View SolutionLet a,b,c be positive real numbers with abc=1 let A =⎡⎢⎣abcbcacab⎤⎥⎦ifATA=I where AT is the transpose of A and I is the identity matrix , then determine the value of a2+b2+c2
View SolutionIf a,b and c are integers and a≥1,b≥2andc≥3. If a+b+c=15, the number of possible solutions of the equation is
View SolutionLet S be the set of 2×2 matrices given by S={A=[abcd],wherea,b,c,d,∈I}, such that AT=A−1 Then
View SolutionIf a,b,c are three positive real numbers then the minimum value of the expression b+ca+c+ab+a+bc is
View SolutionIf a,b, and c are positive integers such that a+b+c≤8, the number of possible values of the ordered triplet (a,b,c) is
View SolutionIf matrix A =⎡⎢⎣abcbcacab⎤⎥⎦ where a,b,c are real positive number ,abc =1 and ATA=I then
Which of the following is/are trueView Solution