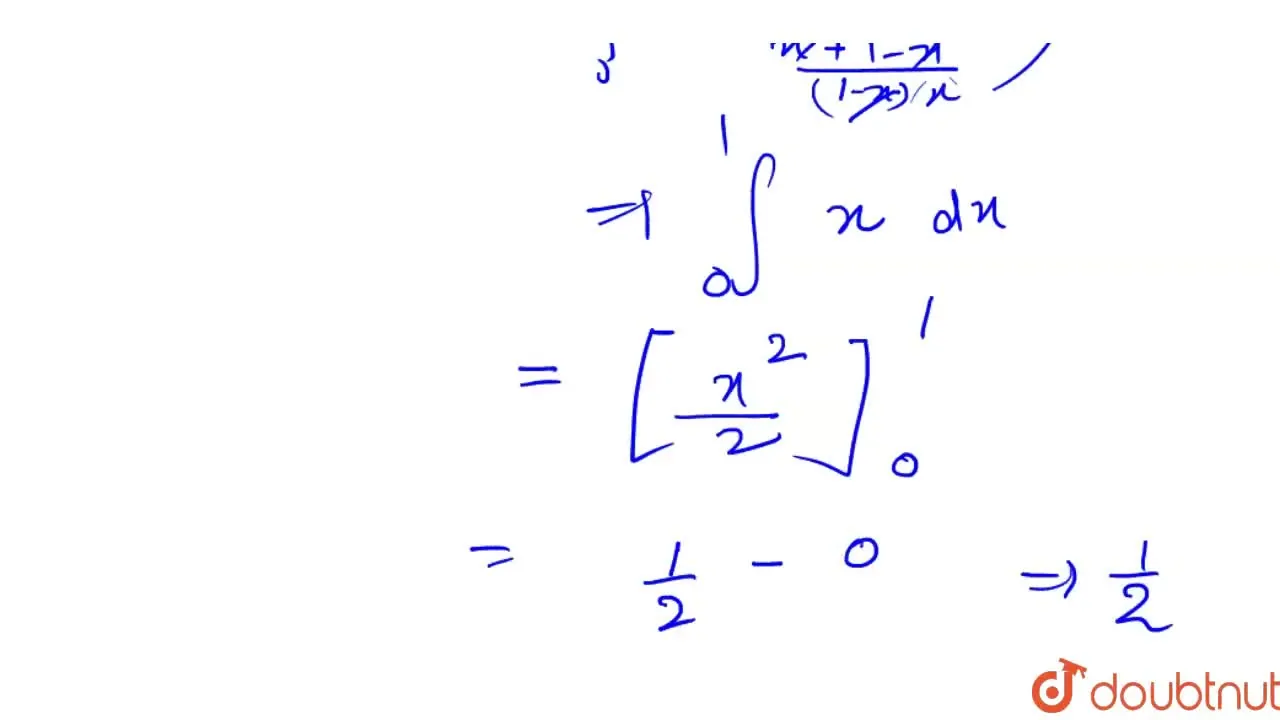If a,b(a<b) be the points of discontinuity of function f(f(f(x))), where f(x)=11−x,x≠1, then ∫baf(x)f(x)+f(1−x)dx=<br><br>
(A) 0 (B) 12 (C) 1 (D) 2
Step by step video & image solution for If a, b (altb) be the points of discontinuity of function f(f(f(x))), where f(x)=1/(1-x),x!=1, then int_a^b f(x)/(f(x)+f(1-x))dx= (A) 0 (B) 1/2 (C) 1 (D) 2 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
If g(x)=f(x)(x−a)(x−b)(x−c),where f(x) is a polynomial of degree <3 , then ∫g(x)dx=∣∣ ∣ ∣∣1af(a)log|x−a|1bf(b)log|x−b|1cf(c)log|x−c|∣∣ ∣ ∣∣÷∣∣ ∣ ∣∣1aa21bb21cc2∣∣ ∣ ∣∣+k dg(x)dx=∣[1,a,−f(a)(x−a)−2],[1,b,−f(b)(x−b)−2],[1,c,−f(c)(x−c)−2]∣∣ ∣ ∣∣−∣∣ ∣ ∣∣1aa21bb21cc2∣∣ ∣ ∣∣
07:22View SolutionIf f(x)=∫xa[f(x)]−1dx and ∫1a[f(x)]−1dx=√2, then
05:21View SolutionSuppose ∣∣∣f'(x)f(x)f''(x)f'(x)∣∣∣=0 is continuously differentiable function with f′(x)≠0 and satisfies f(0)=1 and f'(0)=2 then (lim)x→0f(x)−1x is 1/2 b. 1 c. 2 d. 0
06:21View SolutionIf f(x)=x−1x+1 , then f(f(ax)) in terms of f(x) is equal to (a)f(x)−1a(f(x)−1) (b) f(x)+1a(f(x)−1) f(x)−1a(f(x)+1) (d) f(x)+1a(f(x)+1)
03:03View Solutionf(x)=xx−1 then f(a)f(a+1) is equal to a.f(−a) b.f(1/a) c.f(a2) d.f(−aa−1)
02:59View SolutionIf g(x)=f(x)(x−a)(x−b)(x−c),where f(x) is a polynomial of degree <3 , then ∫g(x)dx=∣∣ ∣ ∣∣1af(a)log|x−a|1bf(b)log|x−b|1cf(c)log|x−c|∣∣ ∣ ∣∣÷∣∣ ∣ ∣∣1aa21bb21cc2∣∣ ∣ ∣∣+k dg(x)dx=∣[1,a,−f(a)(x−a)−2],[1,b,−f(b)(x−b)−2],[1,c,−f(c)(x−c)−2]∣∣ ∣ ∣∣−∣∣ ∣ ∣∣1aa21bb21cc2∣∣ ∣ ∣∣
08:07View SolutionSuppose |[f'(x),f(x)],[f''(x),f'(x)]|=0 is continuously differentiable function with f^(prime)(x)!=0 and satisfies f(0)=1 and f'(0)=2 then (lim)_(x->0)(f(x)-1)/x is 1//2 b. 1 c. 2 d. 0
03:20View Solution