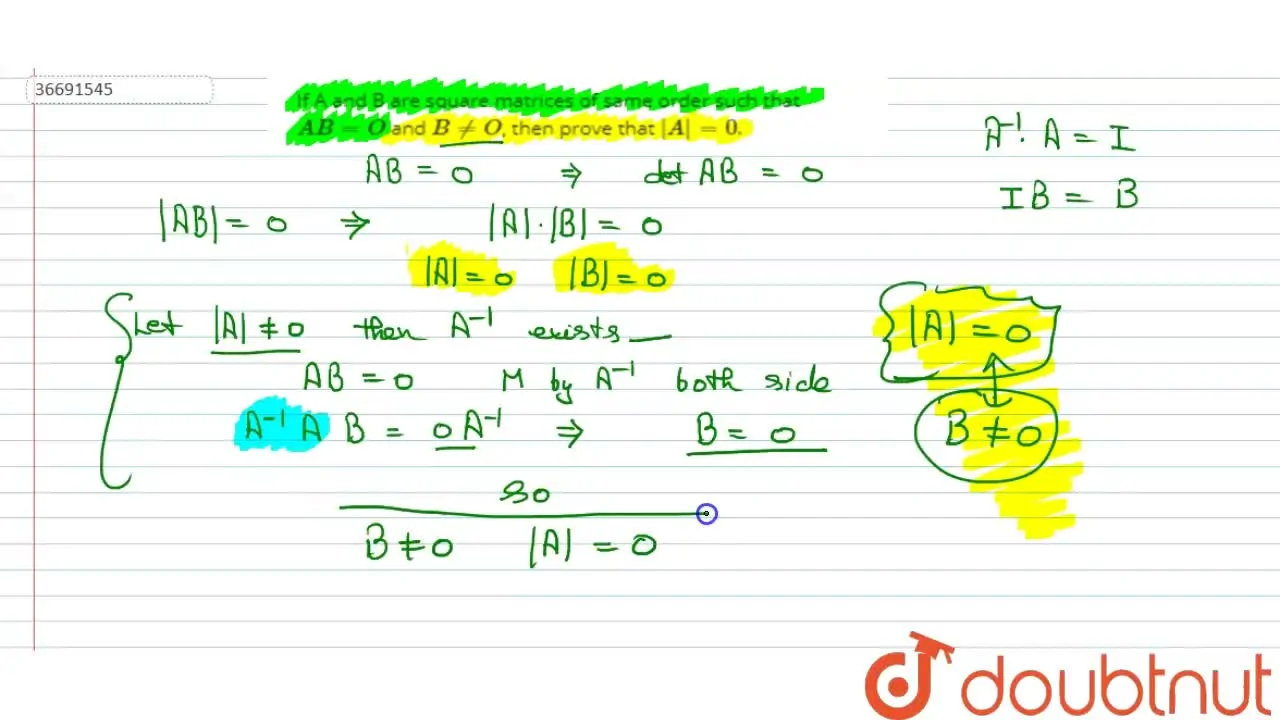
If A and B are square matrices of same order such that AB=O and B≠O, then prove that |A|=0.
We have AB=O
∴|AB|=0
⇒|A||B|=0
⇒|A|=0 or |B|=0
Now, let |A|≠0, then A−1 exists.
Thus, from AB=O,
A−1AB=A−1O
∴IB=O
or B=O
But it is given that B≠O, then |A|=0.
Related Playlists
- BOOK - CENGAGECHAPTER - MATRICESEXERCISE - Exercise 13.15videos
MATRICES
- BOOK - CENGAGECHAPTER - MATRICESEXERCISE - Exercise 13.26videos
MATRICES
- BOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - JEE Previous Year10videos
MATHMETICAL REASONING
- BOOK - CENGAGECHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
Similar Questions
If A and B are square matrices of same order, then
View SolutionIf A and B are square matrices of order 3, then
View SolutionIf A and B are non-zero square matrices of same order such that AB=A andBA=B, then prove that A2=A and B2=B
View SolutionIf A and B are square matrics of the same order then (A−B)2=?
View SolutionIf A and B are square matrics of the same order then (A+B)2=?
View SolutionIf a and B are square matrices of same order such that AB+BA=O, then prove that A3−B3=(A+B)(A2−AB−B2).
View SolutionIf A and B are square matrices of order 2, then (A+B)2 =
View SolutionIf A and B are any two square matrices of the same order than ,
View SolutionIf A and B are square matrics of the same order then (A+B)(A-B)=?
View Solutionif A and B are square matrices of same order such that A = and B = B, where A denotes the conjugate transpose of A, then (AB-BA)* is equal to
View Solution