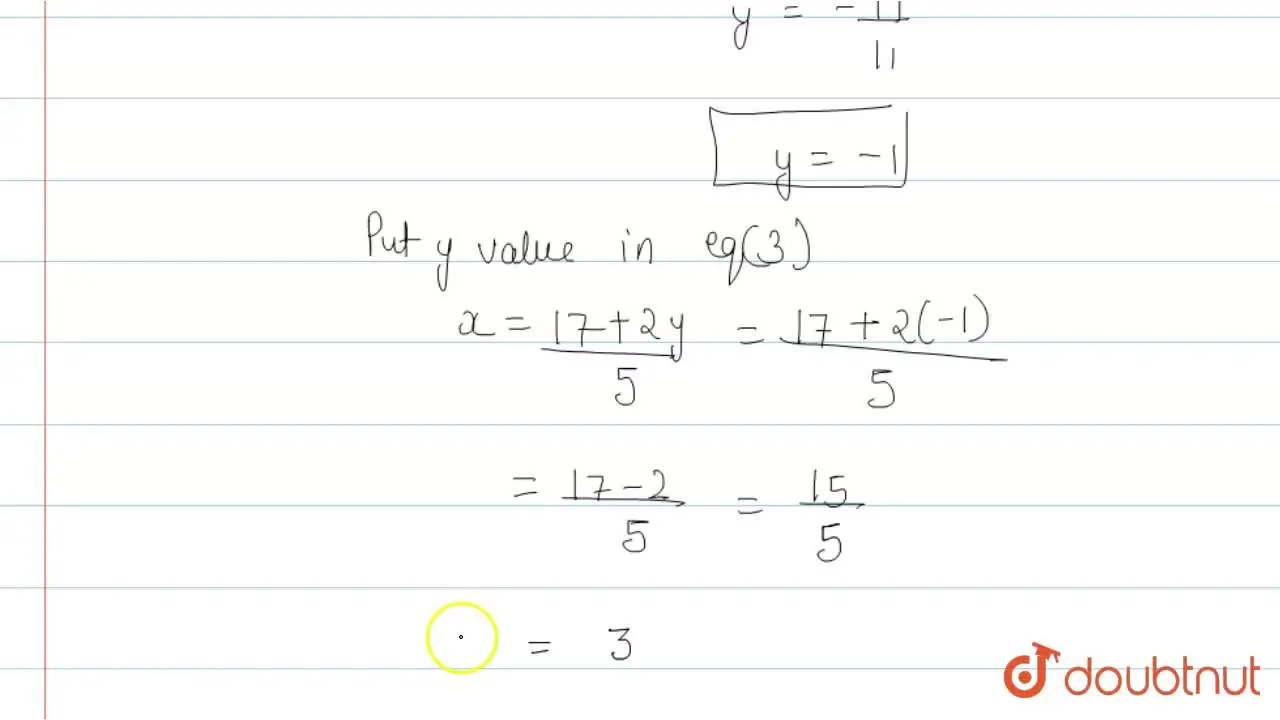If 5x−2y=17and3x+y=8, then find the values of xandy.
Video Solution
Text Solution
Using this method, the two equations are reduced to a single variable equation by substituting the value of one variable obtained from one equation in the other equation.
Step 1: Using the first equation, find x in terms of y.
i.e., 5x−2y=17⇒5x=17+2y
⇒x=17+2y5
Step 2: Substituting the value of x in the equation (2) to find the value of y, i.e., 3x+y=8.
⇒3(17+2y)5+y=8
Step 3 : Simplify the equation in terms of y and find the value of y.
3(17+2y)+5y=8×5
51+6y+5y=40
11y=40−51
11y=−11
⇒y=−1
Step 4: Substituting the value of y obtained in step (3) in equation (1) or (2), we get x =3.
∴ The solution for the given pair of equations is x =3 and y =-1.
|
Updated on:21/07/2023
Related Playlists
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS AND INEQUATIONS EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS30videos
LINEAR EQUATIONS AND INEQUATIONS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS AND INEQUATIONS EXERCISE - SHORT ANSWER TYPE QUESTIONS15videos
LINEAR EQUATIONS AND INEQUATIONS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICESEXERCISE - CONCEPT APPLICATION (Level 3)7videos
INDICES
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MATRICES EXERCISE - Concept Application Level -215videos
MATRICES
Similar Questions
If 3x+5y=21and2x+3y=13, then find the values of xandy.
View SolutionIf 4x+3y=25and5x+2y=26, then find the values of x and y
View SolutionIf 3x+5y=21and2x+3y=13, then find the values of xandy.
View SolutionIf 3x-2y=24 and 2x-3y=18, then find the value of x+y.
View SolutionIF 3x+5Y=9and5x+3y=7 then find the value of x+y
View Solution3x+y=19 and x+3y=1 then find the value of 2x+2y
View SolutionIf 3x + 2y = 10 and 2x + 3y = 15, find the value of x + y.
View SolutionIf 3x+5y =9 and 5x+3y=7, then find the value of x+y.
View SolutionIf 12x+17y=53and17x+12y=63 then find the values of (x+y)
View SolutionIf 7x+5y=-17 and 5x+7y=-19, then find the value of (i) x-y (ii) x+y.
View Solution