If 233 is divided by 17, then the remainder is
(1) 15 (2) 2
(3) 4 (4) 9
17 can be written as 24+1. So, we have to create factors of 24+1 to solve this question.
233=233−29+29−2+2
=29(224−1)+2(28−1)+2
As, a2−1=(a+1)(a−1), we can write our expression as,
=29(212−1)(212+1)+2(24−1)(24+1)+2
=29(212−1)((24)3+(1)3)+2(24−1)(24+1)+2
As, a3+1=(a+1)(a2−a+1), we can write our expression as,
233=29(212−1)(24+1)(28−24+1)(24−1)(24+1)+2
23317=23324+1=29(212−1)(24+1)(28−24+1)(24−1)(24+1)+224+1
Thus, remainder is 2.
Similar Questions
The measure of the angle between the internal and external bisectors of an angle is: (A) 60° (B) 70° (C) 80° (D) 90°
03:22View SolutionIf the difference between mean and m0de is 63, the difference between mean and median is 189 (b) 21 (c) 31.5 (d) 48.5
01:32View SolutionClassify they following curves as open or closed:
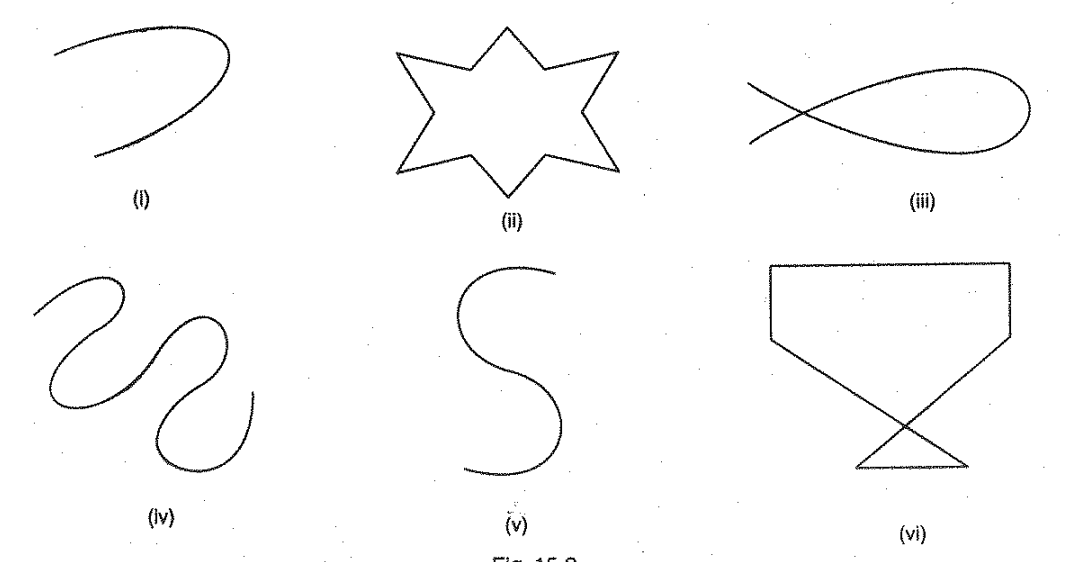 01:44View Solution
01:44View SolutionFollowing are some figures: Classify each of these figures on the basis of the following:(i) Simple curve (ii) Simple closed curve (iii) Polygon (iv) Convex polygon (v)Concave polygon (vi) Not a curve
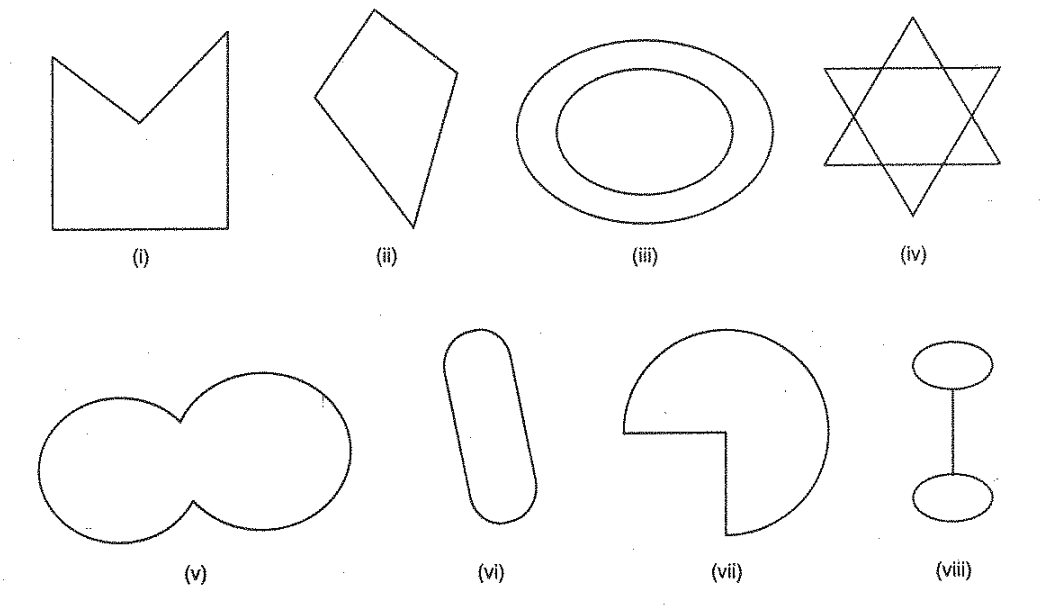 05:11View Solution
05:11View SolutionWhat is a regular polygon? State the name of a regular polygon of
(i) 3 sides
(ii) 4 sides
(iii) 6 sides02:07View SolutionFind the volume in cubic decimetre of each of the cubes whose side is (i)1.5m (ii) 75cm (iii) 2dm 5cm
01:42View SolutionWrite the negation of the following statements and check whether the resulting statements are true,(i) Australia is a continent.(ii) There does not exist a quadrilateral which has all its sides equal,(iii) Every natural number is greater than 0.(iv) The sum of 3 and 4 is 9.
02:43View SolutionA box contains 3 blue, 2 white, and 4 red marbles. If a marble is drawn at random from the box, what is the probability that it will be(i) white? (ii) blue? (iii) red?
02:11View Solution
