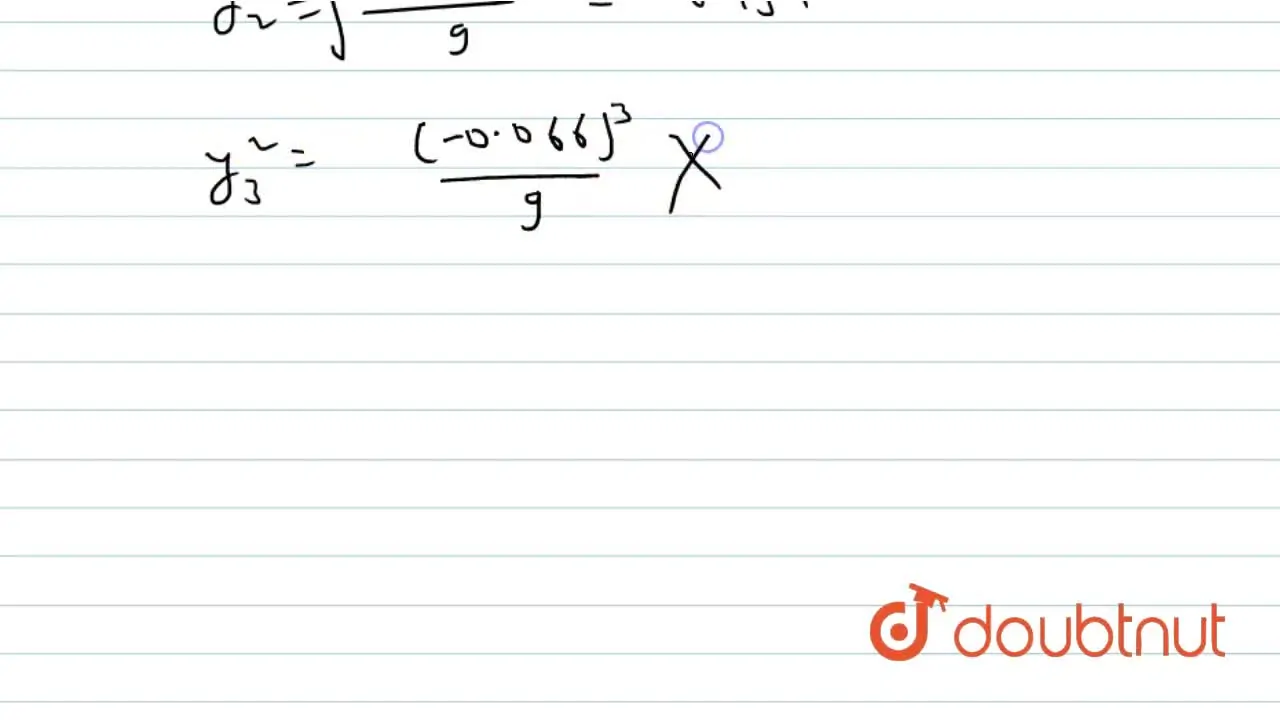(i) Find the point on the curve 9y2=x3 where normal to the curve has non zero x -intercept and both the x intercept and y- intercept are equal.
(ii) If the tangent at (1,1) on y2=x(2−x)2 meets the curve again at P, then find coordinates of P
(iii) The normal to the curve 5x5−10x3+x+2y+6=0 at the point P(0,-3) is tangent to the curve at some other point (s). Find those point(s)?
The correct Answer is:(i) (4,83)(ii)(9/4,3/8)(iii)(1,−1),(−1,−5)
Step by step video, text & image solution for (i) Find the point on the curve 9y^(2)=x^(3) where normal to the curve has non zero x -intercept and both the x intercept and y- intercept are equal. (ii) If the tangent at (1,1) on y^(2)=x(2-x)^(2) meets the curve again at P, then find coordinates of P (iii) The normal to the curve 5x^(5) -10x^(3) +x+2y+6=0 at the point P(0,-3) is tangent to the curve at some other point (s). Find those point(s)? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise -1B6videos
APPLICATION OF DERIVATIVES
- BOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise -1C4videos
APPLICATION OF DERIVATIVES
- BOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Self Practice Problems34videos
APPLICATION OF DERIVATIVES
- BOOK - RESONANCECHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-II: Previously Asked Question of RMO)8videos
COMBINATORICS
Similar Questions
If the tangent at (1, 1) on y2=x(2−x)2 meets the curve again at P then P is
View SolutionFind the point on the curve 9y2=x3, where the normal to the curve makes equal intercepts on the axes.
View SolutionFind the points on the curve 9y2=x3 where normal to the curve makes equal intercepts with the axes.
View SolutionIf the tangent at P (1, 1) on y2=x(2−x)2 meets the curve again at Q then the point Q is
View SolutionThe point on the curve 9y2=x3 where normal to the curve makes equal intercept with the coordinate axes is
View SolutionTangent at (2,8) on the curve y=x3 meets the curve again at Q.Find the coordinates of Q.
View SolutionTangent at P(2,8) on the curve y=x3 meets the curve again at Q.
Find coordinates of Q.View SolutionThe normal to the curve 5x5−10x3+x+2y+6=0 at P(0, -3) meets the curve again at the point
View SolutionTangent at P(2,8) on the curve y=x3 meets the curve again at Q. Find coordinates of Q.
View SolutionThe normal to the curve 5x5−10x3+x+2y+6=0 at the point P(0,-3) meets the curve again at n number of distinct points (other than P then n=
View Solution