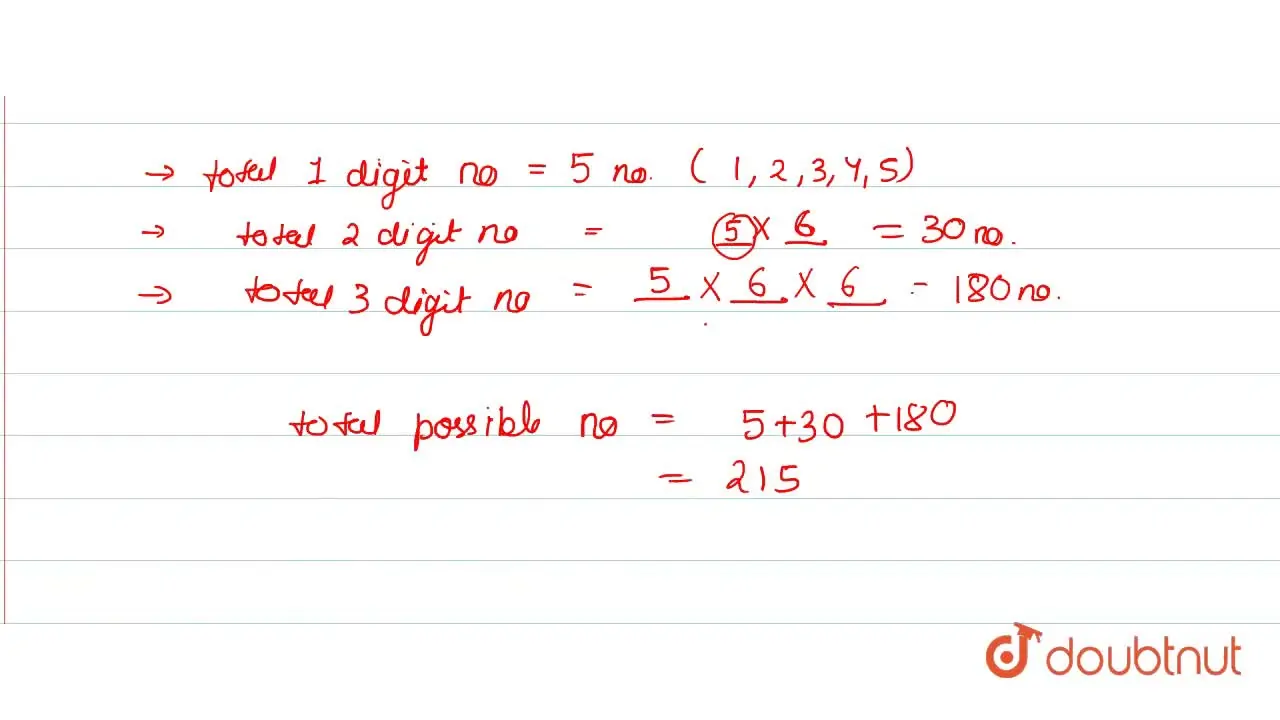How many natural numbers less than 1000 can be formed from the digits 0, 1, 2, 3, 4, 5 when a digit may be repeated any number of times?
The correct Answer is:215
There are 5 one-digit natural natural numbers out of the given digits.
For getting 2-digit natural numbers we cannot put 0 at the ten's place. So, this place can be filled by any of the given five nonzero digits in 5 ways.
The unit's digit can be filled by any of the given six ditits in 6 ways.
So, the number of 2-digit numbers=(5×6)=30.
Similarly, to get a 3-digit number, we cannot put 0 at the hundred's place. So, this place can be filled in 5 ways, each of the ten's and unit's places can be filled in 6 ways.
∴ the number of 3-digit numbers=(5×6×6)=180.
Required number of numbers=(5+30+180)=215.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - PERMUTATIONSEXERCISE - EXERCISE 8C10videos
PERMUTATIONS
- BOOK - RS AGGARWALCHAPTER - PERMUTATIONSEXERCISE - EXERCISE 8D28videos
PERMUTATIONS
- BOOK - RS AGGARWALCHAPTER - PERMUTATIONSEXERCISE - EXERCISE 8A14videos
PERMUTATIONS
- BOOK - RS AGGARWALCHAPTER - PARABOLAEXERCISE - EXERCISE-2210videos
PARABOLA
- BOOK - RS AGGARWALCHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTIONEXERCISE - EXERCISE 423videos
PRINCIPLE OF MATHEMATICAL INDUCTION
Similar Questions
How many natural numbers less than 1000 can be formed form the digits 0,1,2,3,4,5 when a digit may be repeated any number of times?
View SolutionHow many numbers greater than 1000 can be formed from the digits 1, 1, 2, 2,3 ?
View SolutionHow many 4-digit numbers can be formed with the digits 0, 2, 3, 4, 5 when a digit may be repeated any number of times in any arrangement?
View SolutionHow many four-digit numbers can be formed with the digits 1, 2, 3, 4, 5, 6 when a digit may be repeated any number of times in any arrangement ?
View SolutionHow many number lesser than 1000 can be formed from the digits 5,6,7,8 and 9, if no digit is repeated ?
View SolutionHow many different numbers lesser than 10000 can be formed from the digits 0,1,3,6,8,7 and 9, if no digit is repeated ?
View SolutionThe number of numbers less than 1000 than can be formed out of the digits 0,1,2,3,4 and 5, no digit being repeated, as
View SolutionHow many numbers between 10 and 10,000 can be formed by using the digits 1, 2, 3, 4, 5 if
No digit is repeated in any numberView SolutionHow many even numbers greater than 300 can be formed by the digits 1,2,3,4,5 no digit being repeated ?
View SolutionHow many natural numbers less than 1,000 can be formed with digits 1,2,3,4 and 5 if (i) no digit is repeated (ii) repetition of digits is allowed ?
View Solution