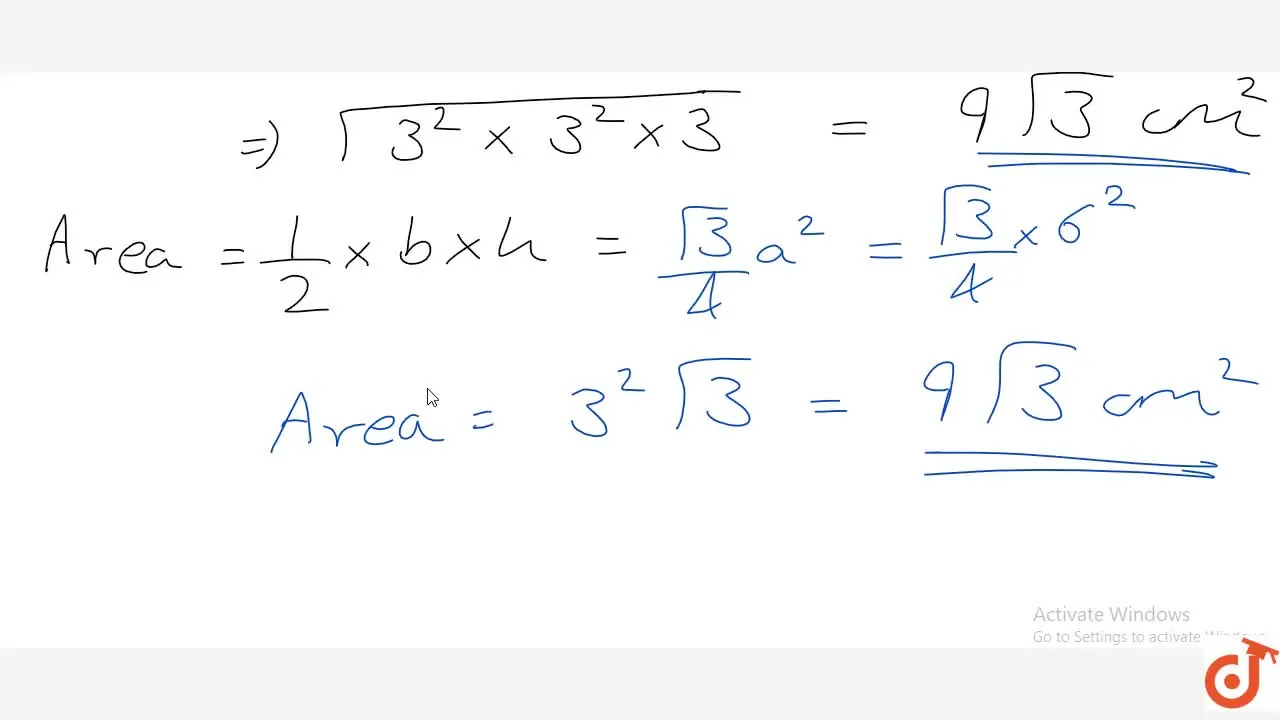Herons's formula
Step by step video, text & image solution for Herons's formula by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Similar Questions
The perimeter of a rhombus is 52 cm. If its one diagonal is 10 cm, find using Heron's formula the area of rhombus.
View SolutionDiscussion OF Ex-12.2 and Examples ||Application OF Heron formula||ProOF OF area OF rhombus=1/2d1d2||Area OF trapezium=1/2(sum OF parallel sides)(distance between parallel sides) || Area OF quadrilateral using Heron's formula
View SolutionThe perimeter of an isosceles triangle is 30 cm and each of the equal sides measures 12 cm. Find the area of the triangle by using Heron's formula.
View SolutionA traffic signal board, indicating 'SCHOOL AHEAD' , is an equilateral triangle with side a. Find the area of the signal board, using Heron's formula. If its perimeter is 180 cm, what will be the area of the signal board?
View SolutionDiscussion OF Exemplar Question and Exercise-12.1||Heron's formula||If side OF triangle is lemda square times OF old triangle||Area OF Equilateral ||Isosceles and Right angle triangle
View SolutionHeron's Formula|Questions|OMR
View SolutionOMR|Heron's Formula|Questions
View SolutionIf perimeter of a triangle is x cm and its sides are p,q and r cm. what will be the area of triangle ? Use the heron's formula.
View SolutionPerimeter|Area |Area Of Triangle|Area Of Triangle - By Heron's Formula|Practice Problem|NCERT Example|OMR
View Solutionusing heron's formula ,find the area of a triangle whose sides are 18cm,24cm and 30 cm
View Solution