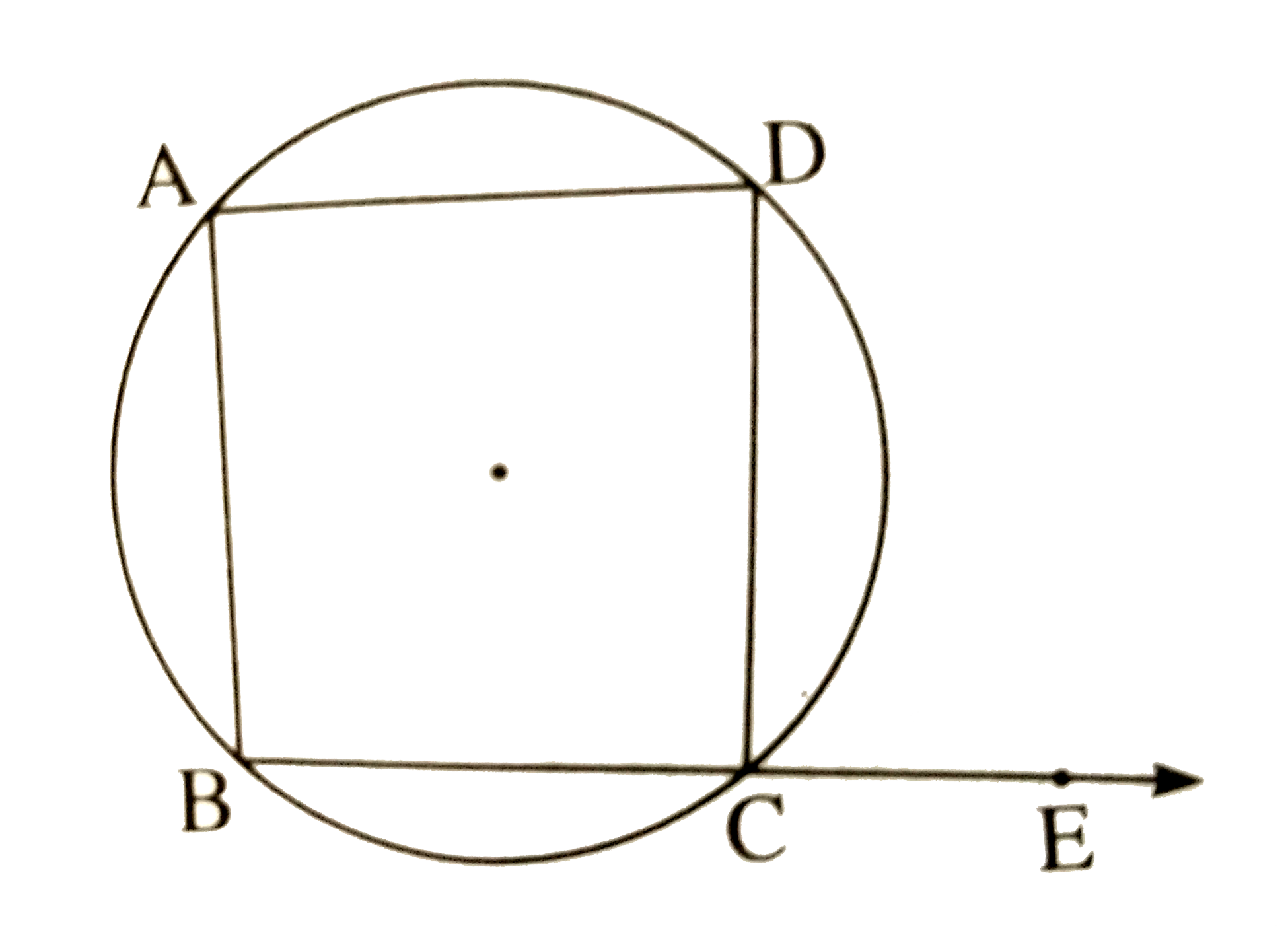
Given :
□ ABCD is cyclic. ∠DCE is an exterior angle of □ ABCD.
To Prove :∠DCE=∠BAD
Complete the proof by filling the boxes.
Video Solution
Text Solution
∠DCE+∠BCD=□ …(Linear pair of angles ) ….(1)
□ ABCD is cyclic
∠BAD+□=180∘ …(Theorem of □ ) ….2)
∴ from (1) and (2), we get,
∠DCE+□=□+∠BCD
∴∠DCE=□
Activity :
∠DCE+∠BCD=180∘ ....(Linear pair of angles ) ...(1)
□ ABCD is cyclic
∠BAD+∠BCD=180∘ ...(Theorem of Cyclic quadrilateral ) ...(2)
∴ from (1) and (2), we get
∠DCE+∠BCD=∠BAD+∠BCD
∴∠DCE=∠BAD
|
Topper's Solved these Questions
- CIRCLEBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:CIRCLEExercise:4.5 (1 mark each)
Explore 7 Videos
- CIRCLEBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:CIRCLEExercise:ASSIGNMENT 4.1
Explore 10 Videos
- CIRCLEBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:CIRCLEExercise:4.3 (1 mark each)
Explore 11 Videos
- CHALLENGING QUESTIONSBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:CHALLENGING QUESTIONSExercise:SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
Explore 1 Video
- COORDINATE GEOMETRY Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:COORDINATE GEOMETRY Exercise:Assignment 6.5
Explore 13 Videos
Similar Questions
Knowledge Check
ABCD is a square and ABE is an equilateral triangle outside the square then
A∠ACE=12∠ABEB∠ACE=∠ABEC∠ACE=2∠ABEDNone of theseABCD is a cyclic parallelogram. The angle ∠B is equal to :
A30∘B60∘C45∘D90∘If the length of diagonal BD of a square ABCD is 4.8 cm, the area of the square ABCD is :
A9.6cm2B11.52cm2C12.52cm2D5.76cm2
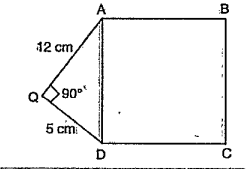
What is the area of the square ABCD shown in the diagram ?
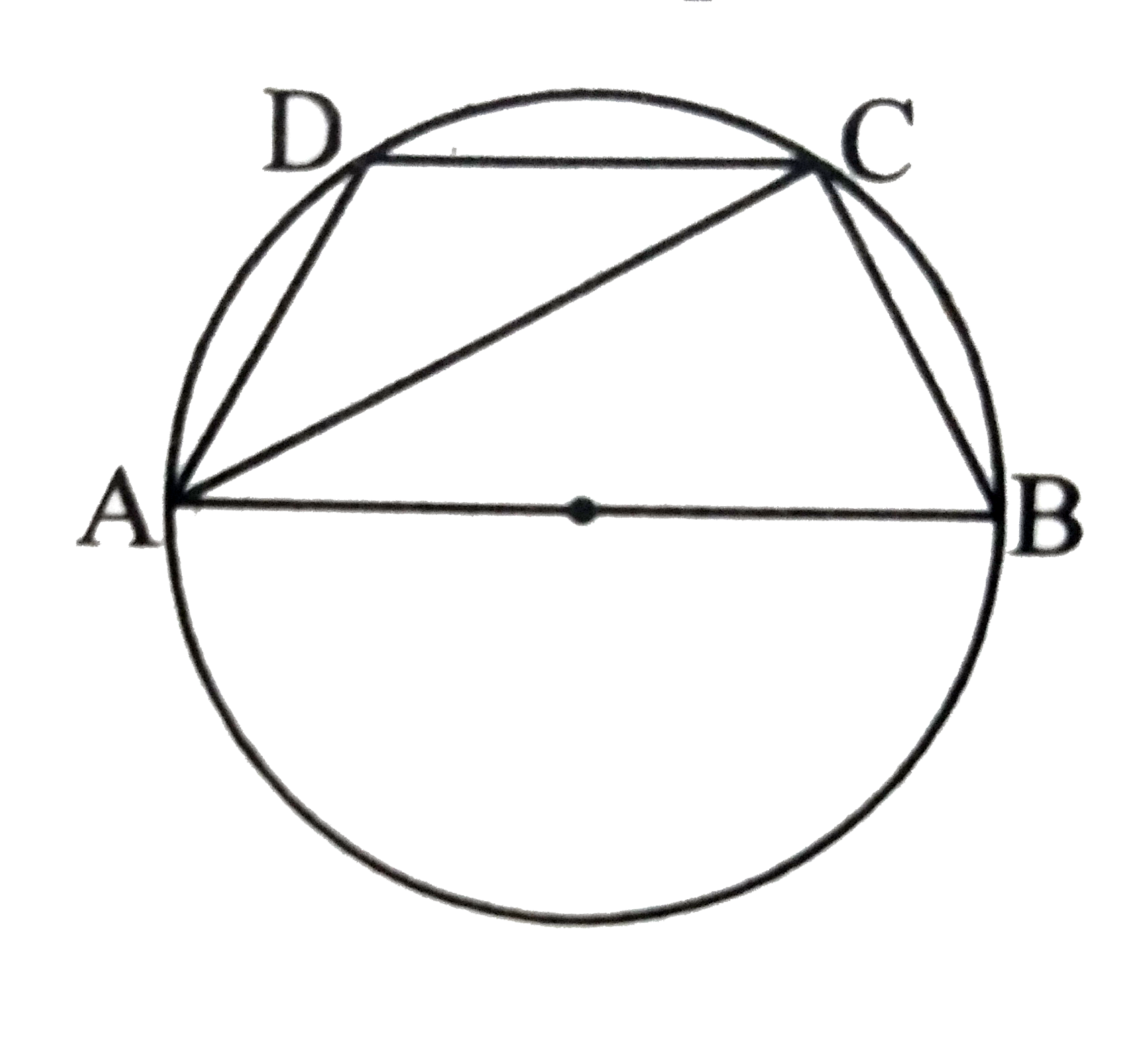
View SolutionIn the figure □ ABCD is a cyclic quadrilateral.Seg AB is a diameter . If ∠ADC=120∘ , complete the following activity to find the measure of ∠BAC.
View Solution
In the figure above, ABCD is a square and PQCD is a rectangle. Find ∠PRC.
View SolutionIf the length of diagonal BD of a square ABCD is 4.8 cm, the area of the square ABCD is :
View SolutionIf the length of the diagonal AC of a square ABCD is 5.2 cm, then the area of the square is :
View Solution


