Give two circles intersecting orthogonally having the length of common chord 24/5 units. The radius of one of the circles is 3 units.
The radius of other circle is
6 units
4 units
2 units
4units
The correct Answer is:2
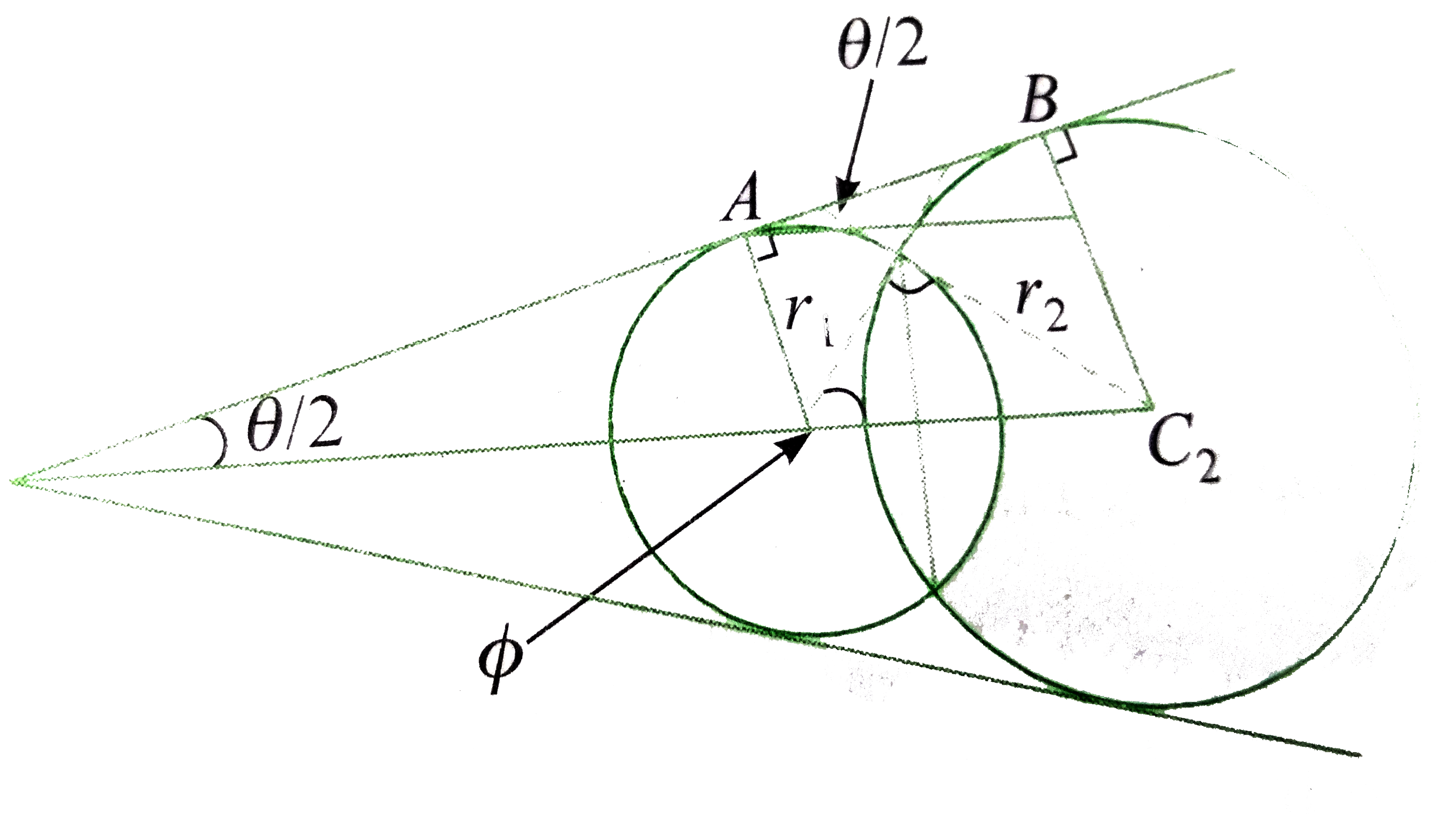
We have sinϕ=d/r1 and cosϕ=d/r2. ( where 2d is the length of the comon chord ). Then,
l=d2r21+d2r22
or d=r1r2√r21+r22
or 2d=2r1r2√r21+r22=245, where r1=3
or d=6r2√9+r22=245
or r2=4
From the figure,
sin.θ2=r2−r1C1C2
where C21C22=r21+r22
or C1C2=5
∴sin.θ2=15
or cos.θ2=√245
∴sinθ=2x15×√245
=4√625
or θ=sin−1.4√625
Also, AB=√C1C22−(r1−r2)2=√25−1=√24
Related Playlists
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE6videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Matrix)1videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)25videos
CIRCLE
- BOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank31videos
BINOMIAL THEORM
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank32videos
CIRCLES
Similar Questions
Give two circles intersecting orthogonally having the length of common chord 24/5 units. The radius of one of the circles is 3 units.
The length of direct common tangent isView SolutionGive two circles intersecting orthogonally having the length of common chord 24/5 units. The radius of one of the circles is 3 units.
The angle between direct common tangents isView SolutionGive two circles intersecting orthogonally having the length of common chord 24/5 units. The radius of one of the circles is 3 units.
The angle between direct common tangents isView SolutionGiven two circles intersecting orthogonally having the length of common chord 245 unit. The radius of one of the circles is 3 units.
If length of direct common tangent is λ units, then λ2 isView SolutionThe circles having radii r1andr2 intersect orthogonally. The length of their common chord is 2r1r2√r12+r12 (b) √r12+r122r1r2 r1r2√r12+r12 (d) √r12+r12r1r2
View SolutionThe circles having radii r1andr2 intersect orthogonally. Find the length of their common chord.
View SolutionThe circles having radii r 1 and r2 intersect orthogonally Length of their common chord is
View SolutionThe circles having radii r1andr2 intersect orthogonally. The length of their common chord is
View SolutionIf two chords having lengths a2−1 and 3(a+1), where a is a constant of a circle bisect each other, then the radius of the circle is
View SolutionTwo circles C1 and C2 intersect in such a way that their common chord is of maximum length. The center of C1 is (1, 2) and its radius is 3 units. The radius of C2 is 5 units. If the slope of the common chord is 34, then find the center of C2.
View Solution

