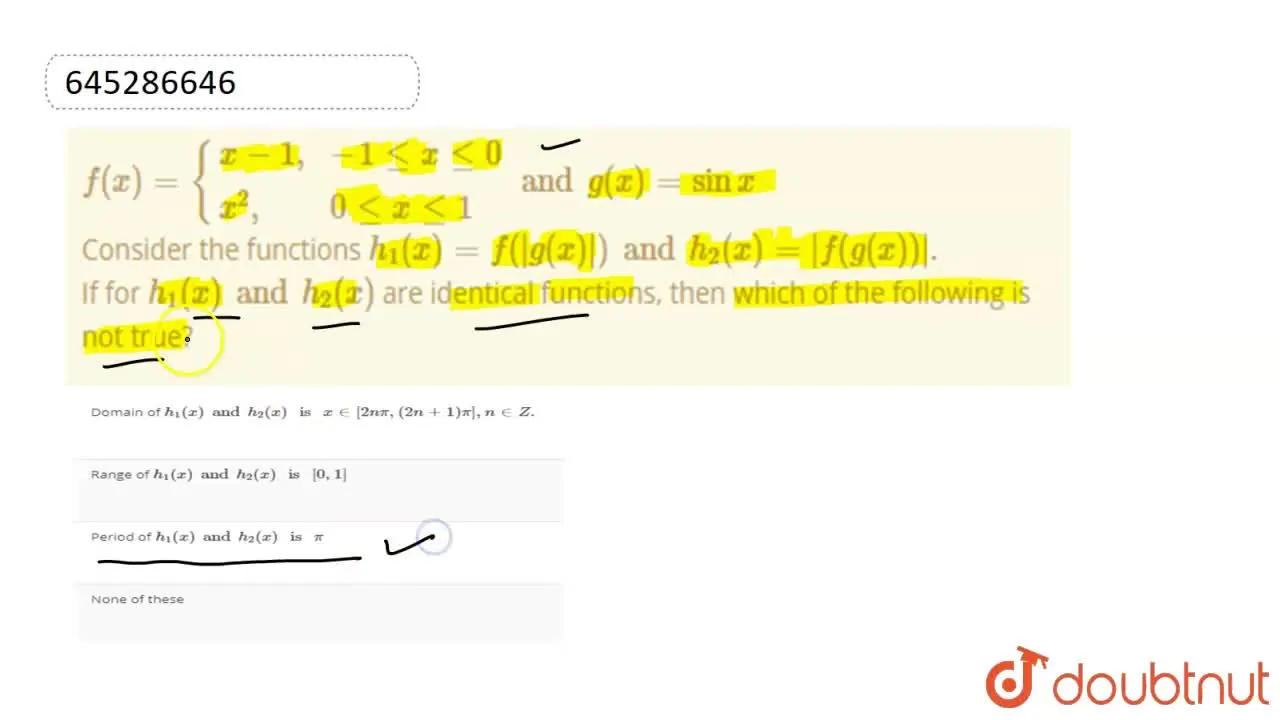
f(x)={x−1,−1≤x≤0x2,0≤x≤1andg(x)=sinx
Consider the functions h1(x)=f(|g(x)|)andh2(x)=|f(g(x))|.
If for h1(x)andh2(x) are identical functions, then which of the following is not true?Solution in Tamil
Domain of h1(x)andh2(x) is x∈[2nπ,(2n+1)π],n∈Z.
Range of h1(x)andh2(x) is [0,1]
Period of h1(x)andh2(x) is π
None of these
The correct Answer is:C
|g(x)|=|sinx|,x∈R
f(|g(x)|)={|sinx|−1,−1≤|sinx|<0(|sinx|)2,0≤(|sinx|)≤1=sin2x,x∈R
f(g(x))={sinx−1,−1≤sinx<0sin2x,0≤sinx≤1
={sinx−1,(2n−1)π<x<2nπsin2x,2nπ≤x≤(2n+1)π,n∈Z.
or |f(g(x))|={sinx−1,(2n−1)π<x<2nπsin2x,2nπ≤x≤(2n+1)π,n∈Z.
For h1(x)≡h2(x)=sin2x,x∈[2nπ,(2n+1)π],n∈Z, and has range [0, 1] for the common domain.
Also, the period is 2π (from the graph).
Related Playlists
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Matrix)9videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Numerical)31videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Multiple)27videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank28videos
Quadratic Equations, Inequalities, Modulus and Logarithms
- BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
Similar Questions
The function f(x) is defined on the interval [0, 1]. Now, match the following lists:
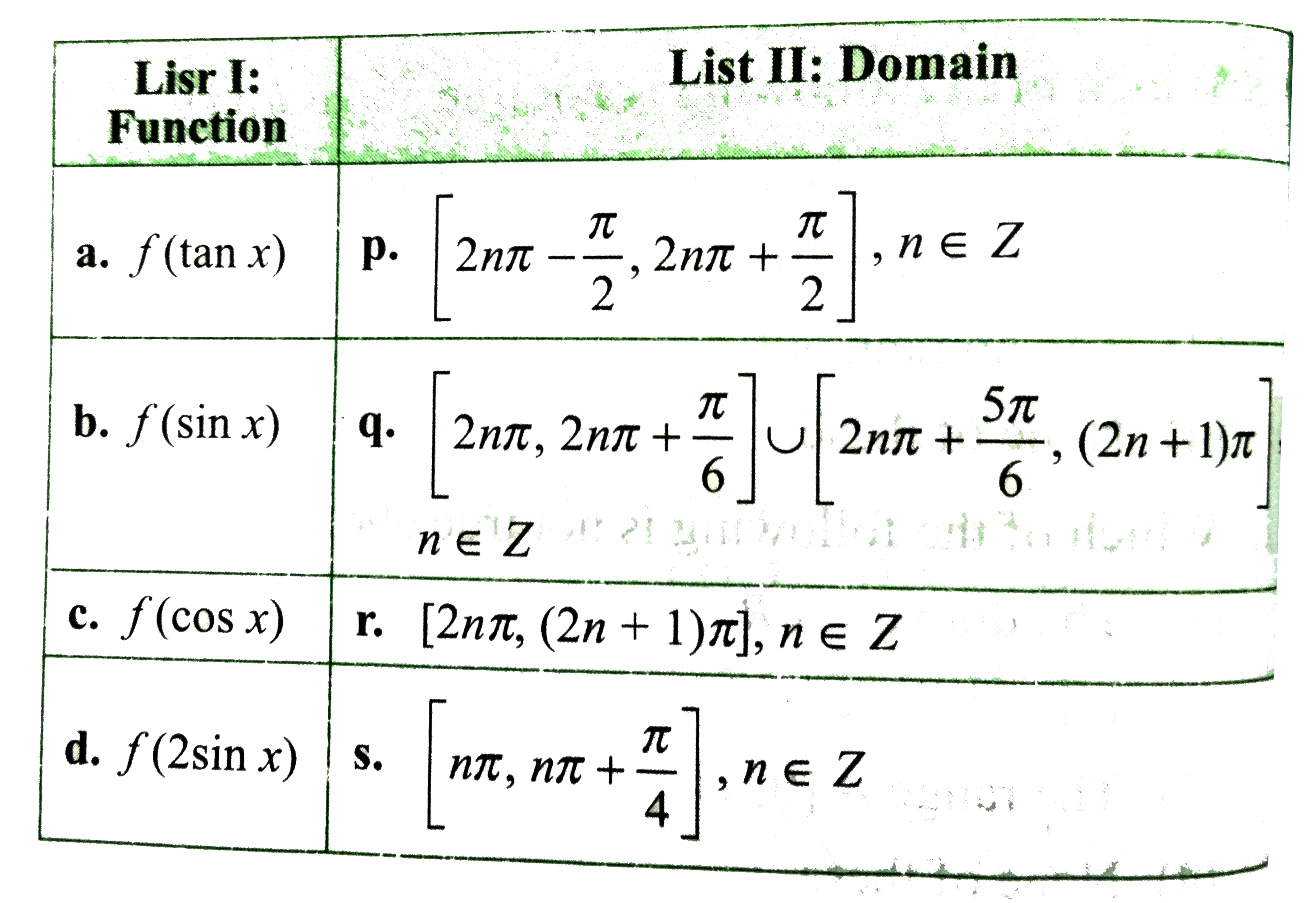 03:52View Solution
03:52View SolutionLet f be a real-valued invertible function such that f(−32xx−2)=5x−2,x≠2. Then value of f−1(13) is________
03:45View SolutionLet f(x)=sec−1[1+cos2x], where [.] denotes the greatest integer function. Then the range of f(x) is
04:56View SolutionLet a,b,c,d be positive integers such that (log)ab=32and(log)cd=54. If (a−c)=9, then find the value of (b−d).
View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj+ˆk and ˆi−ˆj+ˆk, in the order from right-handed system ∀x ∈R, is
03:23View SolutionThe relation f is defined by f(x)={3x+2, 0≤x≤2x3, 2≤x≤5.
The relation g is defined by g(x)={3x+2, 0≤x≤1x3, 1≤x≤5
Show that f is a function and g is not a function02:06View Solutionf(x)={x−1,−1≤x≤0x2,0≤x≤1andg(x)=sinx
Consider the functions h1(x)=f(|g(x)|)andh2(x)=|f(g(x))|.
Which of the following is not true about h1(x)?View Solutionf(x)={x−1,−1≤x≤0x2,0≤x≤1andg(x)=sinx
Consider the functions h1(x)=f(|g(x)|)andh2(x)=|f(g(x))|.
Which of the following is not true about h2(x)?View Solutionf(x)={x−1,−1≤x≤0x2,0≤x≤1andg(x)=sinx
Consider the functions h1(x)=f(|g(x)|)andh2(x)=|f(g(x))|.
If for h1(x)andh2(x) are identical functions, then which of the following is not true?03:05View SolutionLet f(x) and g(x) be two functions given by f(x)=−1|x−1|,−1≤x≤3 and g(x)=2−|x+1|,−2≤x≤2
Then,03:51View SolutionLet f(x)=x3−x2+x+1andg(x) be a function defined by g(x)={Max{f(t):0≤t≤x}0≤x≤13−x1≤x≤2 Then, g(x) is
04:41View SolutionConsider the function f(x)=f(x)={x−1,−1≤x≤0x2,0≤x≤1
and g(x)=sinx.
If h1(x)=f(|g(x)|)
and h2(x)=|f(g(x))|.
Which of the following is not true about h1(x)?04:49View SolutionConsider the function f(x)=f(x)={x−1,−1≤x≤0x2,0≤x≤1
and g(x)=sinx.
If h1(x)=f(|g(x)|)
and h2(x)=|f(g(x))|.
Which of the following is not true about h2(x)?02:43View SolutionThe relation f is defined by f(x)={3x+2, 0≤x≤2x3, 2≤x≤5.
The relation g is defined by g(x)={3x+2, 0≤x≤1x3, 1≤x≤5
Show that f is a function and g is not a function04:31View Solutionf(x)={x−1,−1≤x≤0x2,0≤x≤1andg(x)=sinx
Consider the functions h1(x)=f(|g(x)|)andh2(x)=|f(g(x))|.
then05:54View Solution