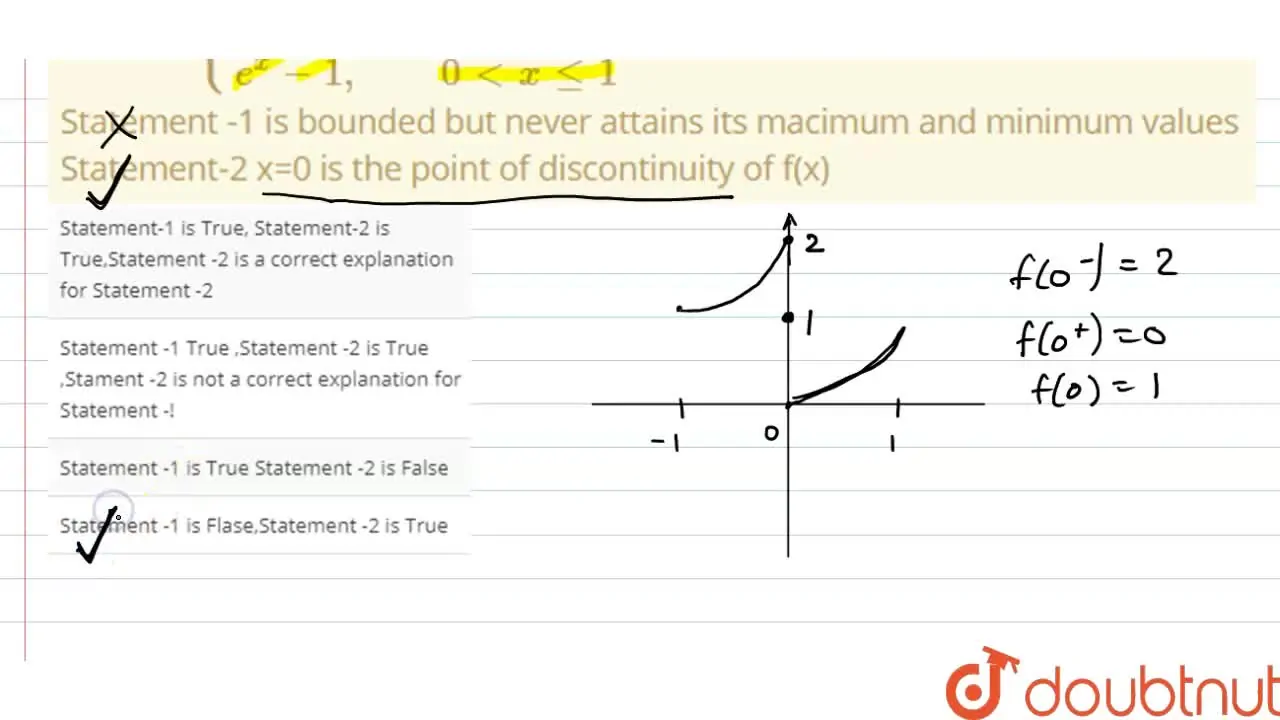
f(x)=⎧⎪⎨⎪⎩ex+1, −1≤x>0ex, x=0ex−1, 0<x≤1
Statement -1 is bounded but never attains its macimum and minimum values
Statement-2 x=0 is the point of discontinuity of f(x)
Statement-1 is True, Statement-2 is True,Statement -2 is a correct explanation for Statement -2
Statement -1 True ,Statement -2 is True ,Stament -2 is not a correct explanation for Statement -!
Statement -1 is True Statement -2 is False
Statement -1 is Flase,Statement -2 is True
The correct Answer is:A
Given that
f(x)=⎧⎪⎨⎪⎩ex+1, −1≤x>0ex, x=0ex−1, 0<x≤1
⇒f'(x)={ex, −1<x<0ex, 0<x<1
It is evident from the graph of f(x) that f(x) is bounded and has 2 and 0 as its maximum and minimum values . Also,f(x) does not attain these values as f(x) is not continuous at x=0
Hence , both the statements are true and statement-2 is a correct explanations of statement-1

Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - MAXIMA AND MINIMA EXERCISE - Exercise50videos
MAXIMA AND MINIMA
- BOOK - OBJECTIVE RD SHARMACHAPTER - MAXIMA AND MINIMA EXERCISE - Chapter Test30videos
MAXIMA AND MINIMA
- BOOK - OBJECTIVE RD SHARMACHAPTER - MAXIMA AND MINIMA EXERCISE - Section I - Solved Mcqs72videos
MAXIMA AND MINIMA
- BOOK - OBJECTIVE RD SHARMACHAPTER - MATHEMATICAL REASONING EXERCISE - Chapter Test20videos
MATHEMATICAL REASONING
- BOOK - OBJECTIVE RD SHARMACHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - Chapter Test21videos
MEASURES OF CENTRAL TENDENCY
Similar Questions
A function is defined as f(x)={ex,x≤0|x−1|,x>0, then f(x) is
View SolutionIf f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩e1x−1e1x+1, for x≠01, for x=0, then f is
View Solutionf(x)e5x−e3xsin2x, if x≠0=1, if x=0} at x = 0 is ,
View SolutionIf f(x)=⎧⎪⎨⎪⎩x,0≤x≤12−ex−1,1<x≤2x−e,2<x≤3 and g'(x)=f(x),x∈[1,3], then
View SolutionProve that the function f(x)={x+1at−1≤x≤0−xat0<x≤1 is discontinuous at the point x=0 and still has the maximum and the minimum value on [-1,1].
View SolutionLet f(x)={ex−1x,x>00,x=0 be a real valued function.
Which of the following statements is/are correct?
1. f(x) is right continuous at x=0.
2. f(x) is discontinuous at x=1.
Seletct the correct answer using the code given below.View Solutionf(x)=⎧⎨⎩e1/x1+e1/xifx≠00ifx=0 at x=0
View SolutionLet f(x)={ex−1x,x>00,x=0 be a real valued function.
Which one of the following statements is correct?View SolutionIf f(x)={1e1/x,x≠00,x=0 then
View Solutionf(x)=⎧⎨⎩e1/x1+e1/xifx≠00ifx=0atx = 0
View Solution