The value of k for which the function defined as f(x)=⎧⎨⎩1−coskxxsinxifx≠012ifx=0 continuous at x=0
The correct Answer is:N/a
We have, f(x)=⎧⎨⎩1−coskxxsinxifx≠012ifx=0 at x=0
At x=0,LHL=limh→0−1−coskxxsinx=limh→01−cos(0−h)(0−h)sin(0−h)
=limh→01−cos(−kh)−hsin(−h)
=limh→01−coskhhsinh,[∵cos(−θ)=cosθ,sin(−θ)=−sinθ]
=limh→01−1+2sin2'kh2hsinh,[∵cosθ=1−2sin2'θ2]
=limh→02sin2'kh2hsinh
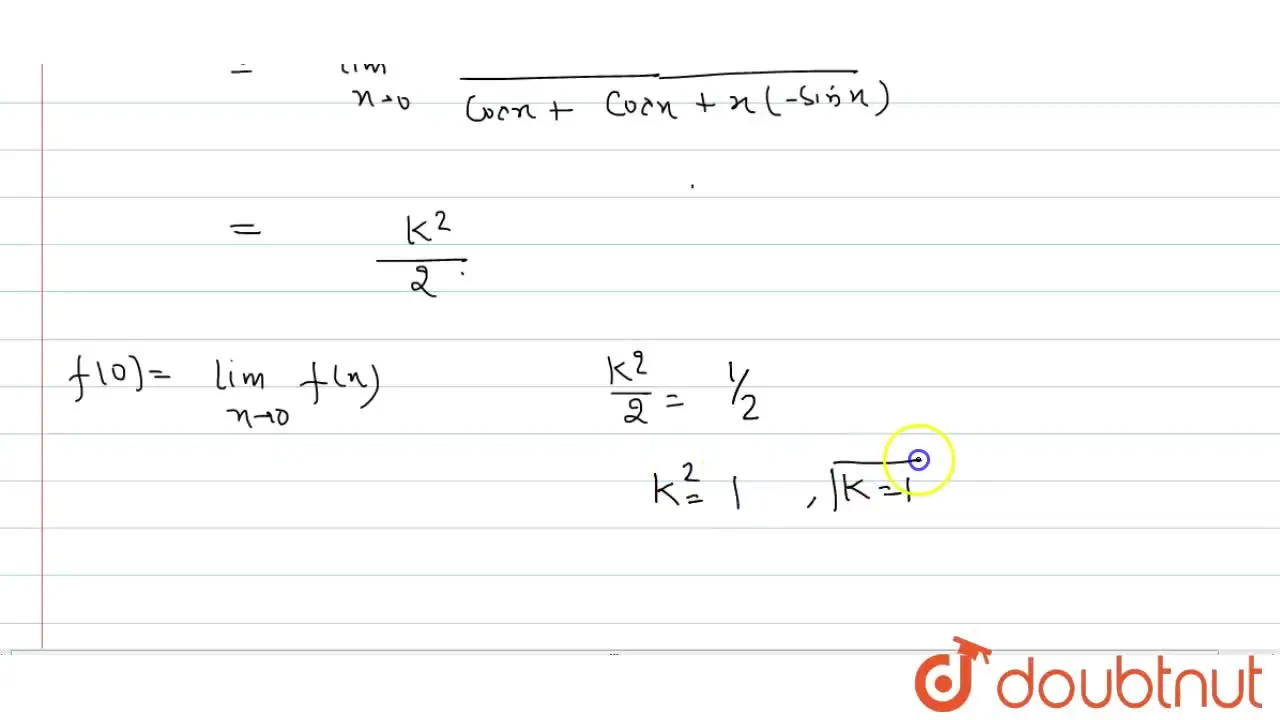
=limh→02sin'kh2kh2.sin'kh2kh2.1sinhh.k2h/4h
=2k24=k22 , [∵limh→0'sinhh=1]
Also, f(0)=12⇒k22=12⇒k±1
Related Playlists
Similar Questions
The value of k for which the function defined as f(x)=⎧⎨⎩1−coskxxsinxifx≠012ifx=0 continuous at x=0
View Solutionf(x)=⎧⎨⎩1−coskxxsinxifx≠012ifx=0 at x=0
View Solutionf(x)=⎧⎨⎩1−cosAxxsinxifx≠012ifx=0 at x=0
View SolutionThe value of k(k<0) for which the function is continuous at x=0
f(x)=⎧⎨⎩1−coskxxsinx,x≠012,x=0View SolutionIf the function f(x)=⎧⎨⎩1−coskxxsinxx≠012x=0 is
continuous at x = 0, then the value (s) of k are:View SolutionFor what value of k, the function defined by
f(x)={log(1+2x)sinx∘x2,for x≠0k,for x=0
is continuous at x = 0 ?View SolutionIf f(x) = {1−cosxxx≠0xx=0 is continuous at x =0 then the value of k is
View SolutionThe value of λ that makes the function f(x)={(cosx)1/sinxx≠0λx=0 continuous at x = 0 is:
View SolutionThe function f defined by f(x)={sinx2xx≠00x=0 is
View SolutionIf the function defined by f(x)={sin3x2x;x≠0k+1;x=0 is continuous at x=0, then k is
View Solution