From the top of a building, the angle of elevation and depression of top and bottom of a tower are 60∘and30∘ respectively. If the height of the building is 5 m, then find the height of the tower.
10√3m
15 m
15√3m
20 m
The correct Answer is:D
AB be the height of the building.
∴AB=5 m(given)
Let PQ be the height of the tower.
In ΔABP,
tan30∘=ABAP⇒1√3=5AP.
∴=5√3⇒∴BR=5√3 m
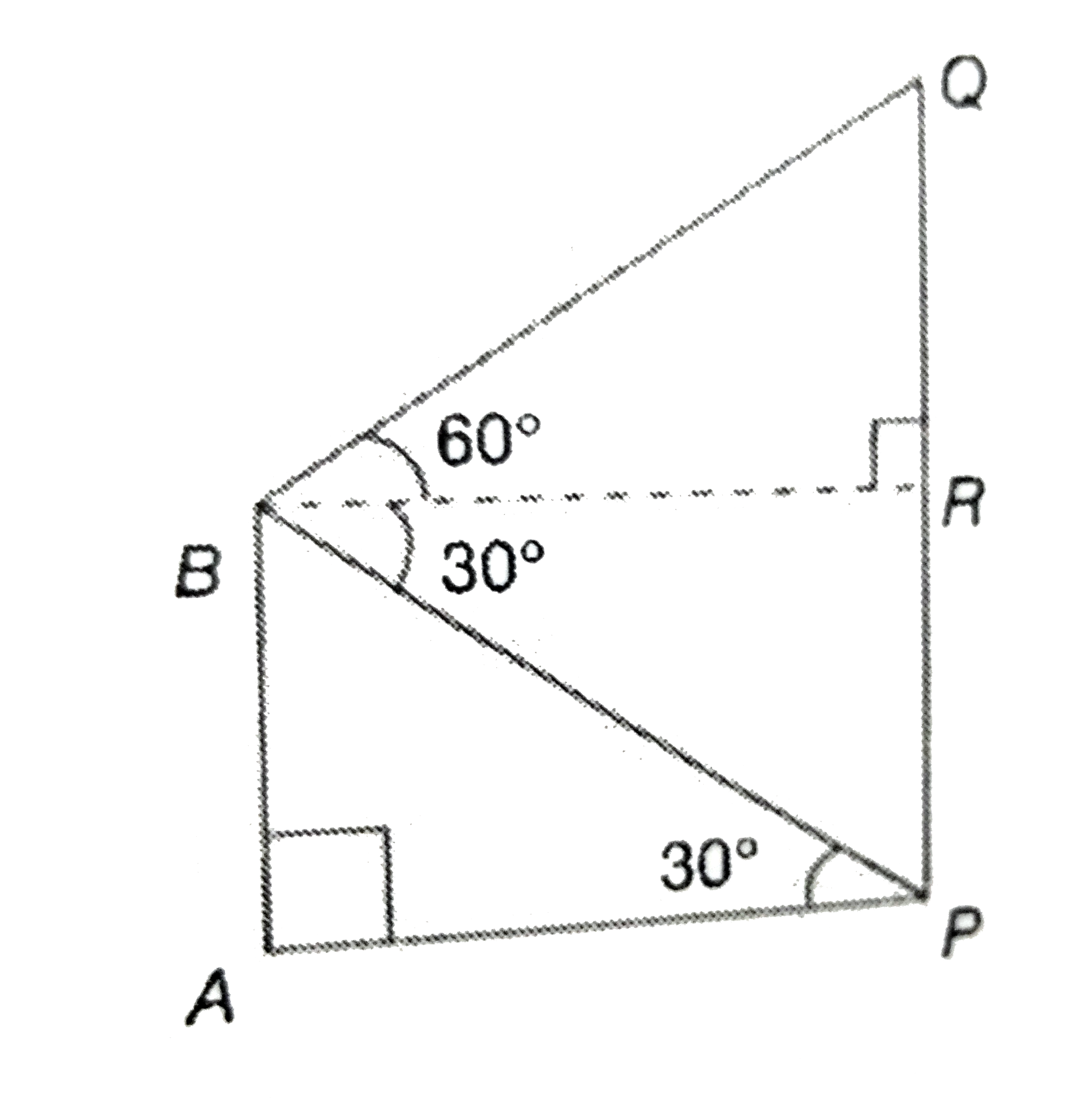
In ΔBQR,tan60∘=QRBR
√3=QR5√3⇒QR=15m
From the figure, PQ = PR + QR
=5 + 15 = 20 m.
Related Playlists
Similar Questions
From the top of a building, the angle of elevation and depression of top and bottom of a tower are 60∘and30∘ respectively. If the height of the building is 5 m, then find the height of the tower.
View SolutionWhen one looks from the foot and the top of a tower from the roof of a building, the angles of elelvation and depression are of 63∘and27∘ respectively. If the height of the building is 20 metres, find the height of the tower. (tan63∘=2)
View SolutionFrom the top of a cliff 90 m high, the angles of depression of the top and bottom of a tower are observed to be 30∘ and 60∘ respectively. The height of the tower is :
View SolutionFrom the top of a cliff 90 m high, the angles of depression of the top and bottom of a tower are observed to be 30∘ and 60∘ respectively. The height of the tower is :
View SolutionIf from the top of a tower 80 meters high the angles of depression of the top and bottom of a house are 30∘and45∘ respectively, then the height of the house is
View SolutionFrom the top of a building 60 metre high ,the angles of depression of the top and bottom of a tower are observed to be 30∘and60∘ respectively.The height of the tower in metre is :
View SolutionFrom the top of a 60 m high building, the angles of depression of the top and the bottom of a tower are 45∘ and 60∘ respectively. Find the height of the tower. [Take √3=1.73]
View SolutionThe angles of elevation of the top of a building from the top and bot tom of a tree are 30∘and60∘ respectively .If the height of the tree is 50 m , then what is the height of the building ?
View SolutionThe angles of elevation of the top of a building from the top and bot tom of a tree are 30∘and60∘ respectively .If the height of the tree is 50 m , then what is the height of the building ?
View SolutionFrom the top of a cliff 90 m high, the angles of depression of the top and bottom of a twoer are observed to be 30∘ and 60∘ respectively. The height of the tower is :
View Solution


