For the matrix A=⎡⎢⎣11112−3213⎤⎥⎦. Show that A3−6A2+5A+11I=0. Hence, find A−1.
Video Solution
Text Solution
Given A=⎡⎢⎣11112−3213⎤⎥⎦.
To proveA3−6A2+5A+11I=0
A2=⎡⎢⎣11112−3213⎤⎥⎦⎡⎢⎣11112−3213⎤⎥⎦
A2=⎡⎢⎣1+1+21+2−11−3+31+2−61+4+31−6−92−1+62−2−32+3+9⎤⎥⎦
=>A2=⎡⎢⎣421−38−147−314⎤⎥⎦
Now, A3=A2A
=⎡⎢⎣421−38−147−314⎤⎥⎦⎡⎢⎣11112−3213⎤⎥⎦
=⎡⎢⎣4+2+24+4−14−6+3−3+8−28−3+16+14−3−24−427−3+287−6−147+9+42⎤⎥⎦
=⎡⎢⎣871−2327−6932−1358⎤⎥⎦
Consider A3−6A2+5A+11I
=⎡⎢⎣871−2327−6932−1358⎤⎥⎦−6⎡⎢⎣421−38−147−314⎤⎥⎦+5⎡⎢⎣11112−3213⎤⎥⎦+11⎡⎢⎣100010001⎤⎥⎦
=⎡⎢⎣871−2327−6932−1358⎤⎥⎦−⎡⎢⎣24126−1848−8442−1884⎤⎥⎦+⎡⎢⎣555510−1510515⎤⎥⎦+⎡⎢⎣110001100011⎤⎥⎦
=⎡⎢⎣8−24+5+117−12+51−6+5−23+18+527−48+10+11−69+84−1532−42+10−13+18−558−84+15+11⎤⎥⎦
=⎡⎢⎣000000000⎤⎥⎦
⇒A3−6A2+5A+11I=0.........(1)
for A−1
Multiplying eq(1) by A−1, we get
A3A−1−6A2A−1+5∀−1+11A−1I=0
⇒A2−6A+5I+11A−1=0
⇒11A−1=−A2+6A−5I
Substituting the values in above eq
11A−1=−⎡⎢⎣421−38−147−314⎤⎥⎦+6⎡⎢⎣11112−3213⎤⎥⎦−5⎡⎢⎣100010001⎤⎥⎦
=⎡⎢⎣−4−2−13−814−73−14⎤⎥⎦+⎡⎢⎣666612−1812618⎤⎥⎦−⎡⎢⎣500050005⎤⎥⎦
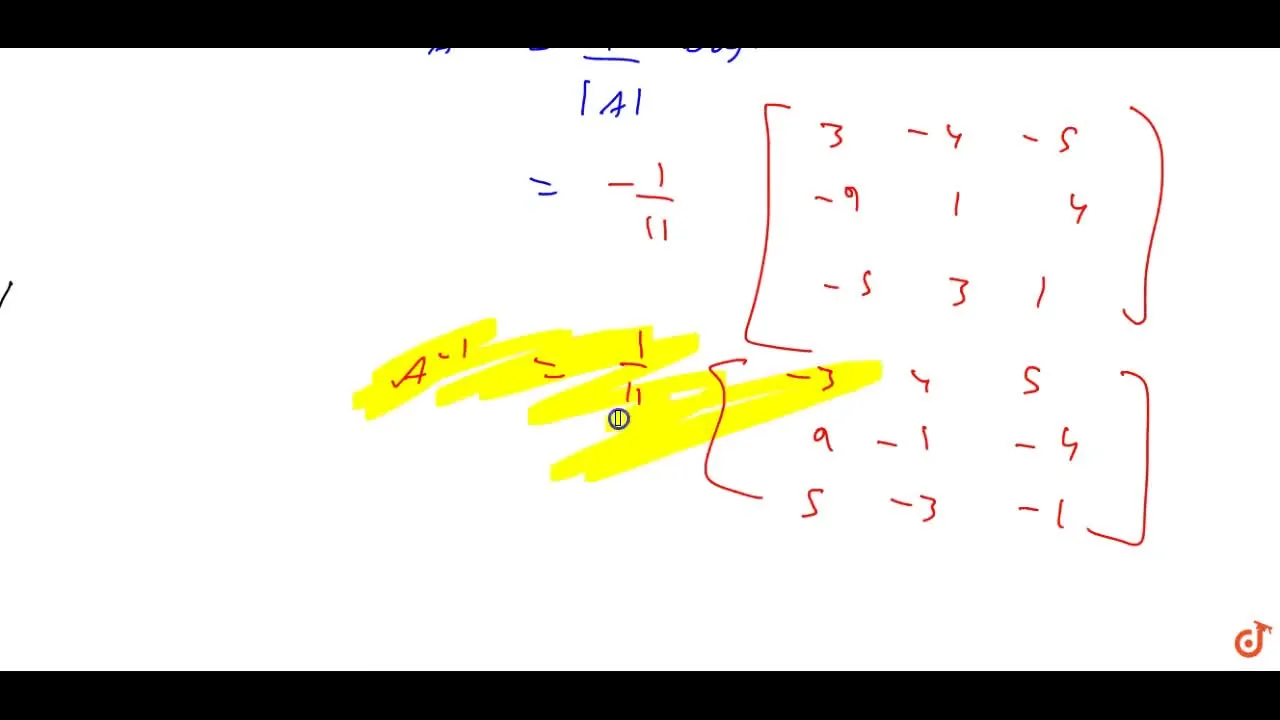
=⎡⎢⎣−4+6−5−2+6−1+63+6−8+12−514−18−7+123−6−14+18−5⎤⎥⎦
⇒A−1=111⎡⎢⎣−3459−1−45−3−1⎤⎥⎦
|
Updated on:21/07/2023
Related Playlists
- BOOK - NCERTCHAPTER - DETERMINANTSEXERCISE - EXERCISE 4.18videos
DETERMINANTS
- BOOK - NCERTCHAPTER - DETERMINANTSEXERCISE - EXERCISE 4.615videos
DETERMINANTS
- BOOK - NCERTCHAPTER - DETERMINANTSEXERCISE - Exercise 4.216videos
DETERMINANTS
- BOOK - NCERTCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - QUESTION3videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - NCERTCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - EXERCISE 9.112videos
DIFFERENTIAL EQUATIONS
Similar Questions
For the matrix A=⎡⎢⎣11112−32−13⎤⎥⎦ . Show that A3−6A2+5A+11 I3=O . Hence, find A−1 .
View SolutionFor the matrix A=∣∣ ∣∣11112−32−13∣∣ ∣∣, then that A3−6A2+5A+11I=0. find A−1
View SolutionIf A=⎡⎢⎣2−11−12−11−12⎤⎥⎦ show that A2−5A+4I=0
Hence find A−1View SolutionIf A=[3112], show that A2−5A+5I=0. Hence, find A−1.
View SolutionIf A=[31−12] then show that A2−5A+7I=0 Hence find A−1
View SolutionIf A=⎡⎢⎣2−11−12−11−12⎤⎥⎦.Verify that A3−6A2+9A−4I=0and hence find A−1.
View SolutionIf A=[31−12], show that A2−5A+7I=O. Hence, find A−1.
View SolutionIf A=[2−113] , then show that A2−5A+7I2=O, hence find A−1.
View SolutionIf A=⎡⎢⎣3−342−340−11⎤⎥⎦2-3 41 then show that A−1=A1.
View SolutionFor the matrix A=⎡⎢⎣11112−3213⎤⎥⎦. Show that A3−6A2+5A+11I=0. Hence, find A−1.
View Solution