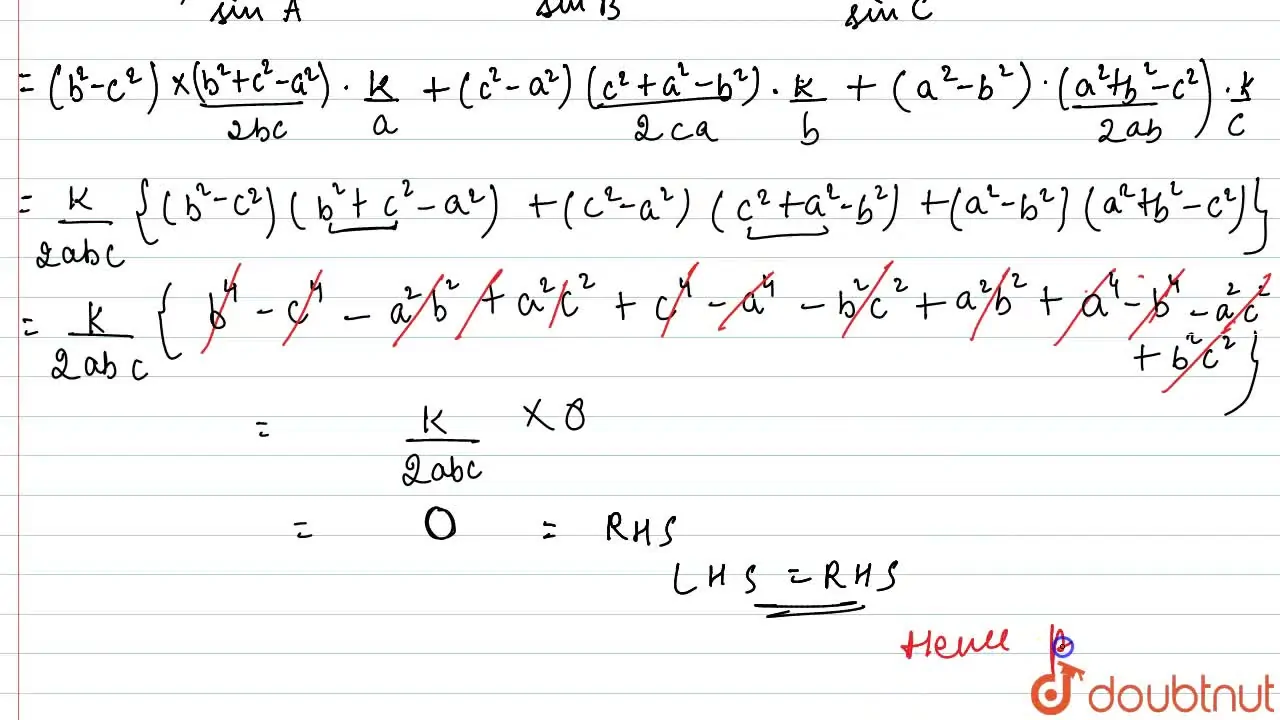For any triangle ABC, prove that(b2−c2)cotA+(c2−a2)cotB+(a2−b2)cotC=0
Video Solution
Text Solution

We have to prove that (b2–c2)cotA+(c2–a2)cotB+(a2–b2)cotC=0
∵ from sine rule, we know that a=ksinA,b=ksinBandc=ksinC
∴(b2–c2)cotA=k2(sin2B–sin2C)cotA
∵sin2B–sin2C=sin(B+C)sin(B–C)
∴(b2–c2)cotA=k2sin(B+C)sin(B–C)cotA
∵B+C=π–A
∴(b2−c2)cotA=k2sinAsin(B−C)cosAsinA
=−k2sin(B−C)cos(B+C)
=−k22[2sin(B−C)cos(B+C)]
⇒(b2−c2)cotA=−k22[sin2B−sin2c].........(i)
similarly (c2−a2)cotB=−k22[sin2C−sin2A].........(ii)
(a2−b2)cotC=−k22[sin2A−sin2B].........(iii)
adding equations(i),(ii) and (iii),
we get (b2–c2)cotA+(c2–a2)cotB+(a2–b2)cotC=0
|
Updated on:21/07/2023
Related Playlists
Similar Questions
In a ΔABC, prove that: (b2−c2)cotA+(c2−a2)cotB+(a2−b2)cotC=0
View SolutionFor any triangle ABC, prove thata(bcosC−ccosB)=b2−c2
View SolutionFor any triangle ABC, prove that a(bcosC−ccosB)=b2−c2
View SolutionIn any △ABC, prove that (b2−c2)cotA+(c2−a2)cotB+(ca−b2)cotC=0
View SolutionIn any ΔABC, prove that
(b2−c2)cotA+(c2−a2)cotB+(a2−b2)cotC=0View SolutionFor any triangle ABC, prove that a(bcosC−osB)=b2−c2
View SolutionFor any triangle ABC, prove thatsin(B−C)sin(B+C)=b2−c2a2
View SolutionIn any triangle ABC, prove that:Δ=b2+c2−a24cotA .
View SolutionFor any triangle ABC, prove thatsin(B−C)2=b−ca(cosA2)
View SolutionFor any triangle ABC, prove thatb2−c2a2sin2A+c2−a2b2sin2B+a2−b2c2sin2C=0
View Solution