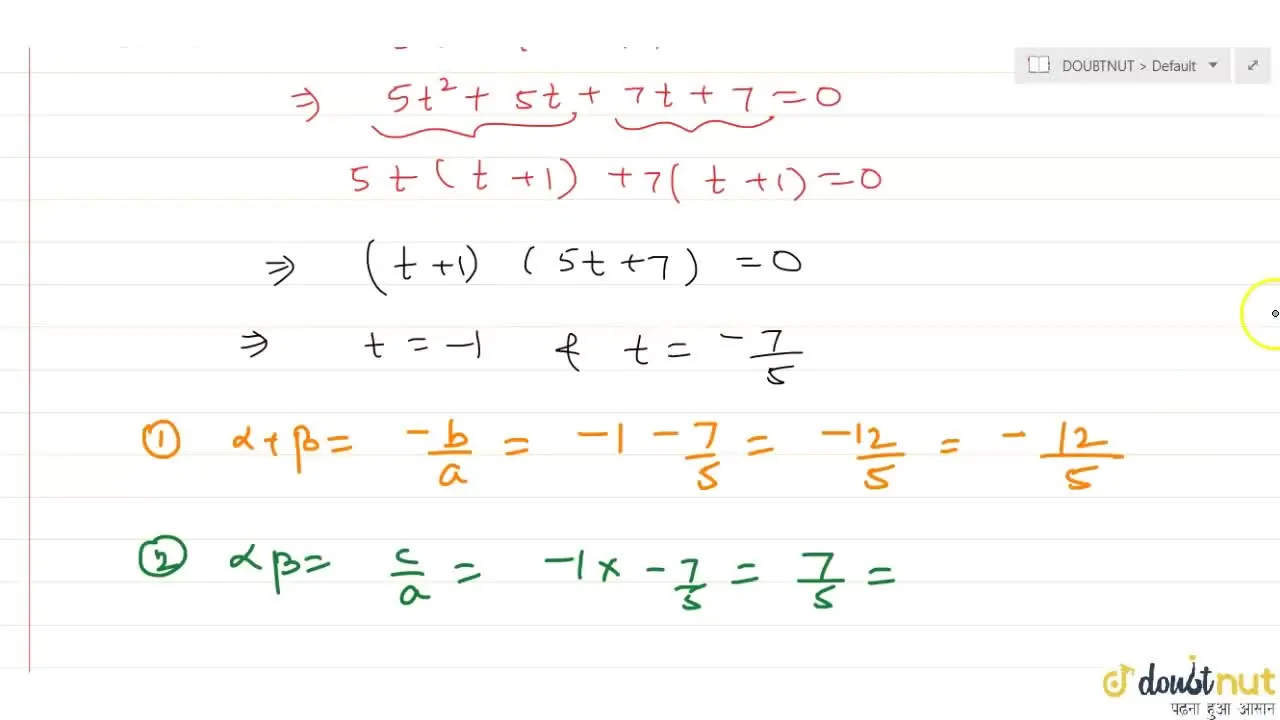Find the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials
(iii) 5t2+12t+7.
Let f(t)=5t2+12t+7
=5t2+7t+5t+7 [by splitting the middle term]
=t(5t+7)+1(5t+7)
=(5t+7)(t+1)
So, the value of 5t2+12t+7 is zero when 5t+7 or t+1=0
i.e., when t=−75 or t=−1.
So, the zeroes of 5t2+12t+7 are −7/5 and -1.
∴ Sum of zeroes =−75−1=−125
=(−1)(Coefficient of tCoefficient oft2)
and product of zeroes =(−75)(−1)=75
=(−1)2(Constant termCoefficient oft2)
Hence, verified the relations between the zeroes and the coefficients of the polynomial.
Related Playlists
Similar Questions
Find the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials
(ii) 3x2+4x−4View SolutionFind the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials
(i) 4x2−3x−1View SolutionFind the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials (iv) t3−2t2−15t.
View SolutionFind the zeroes of the following polynomials factorisation method and verify the relations between the zeroes and the coefficients of the polynomials.
5t2+12t+7View SolutionFind the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials
(viii) v2+4√3v−15View SolutionFind the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials
(vii) 2s2−(1+2√2)s+√2View SolutionFind the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials
(ix) y2+32√5y−5View SolutionFind the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials (vi) 4x2+5√2x−3.
View SolutionFind the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials
(x) 7y2−113y−23View SolutionFind the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials
(v) 2x2+72x+34View Solution