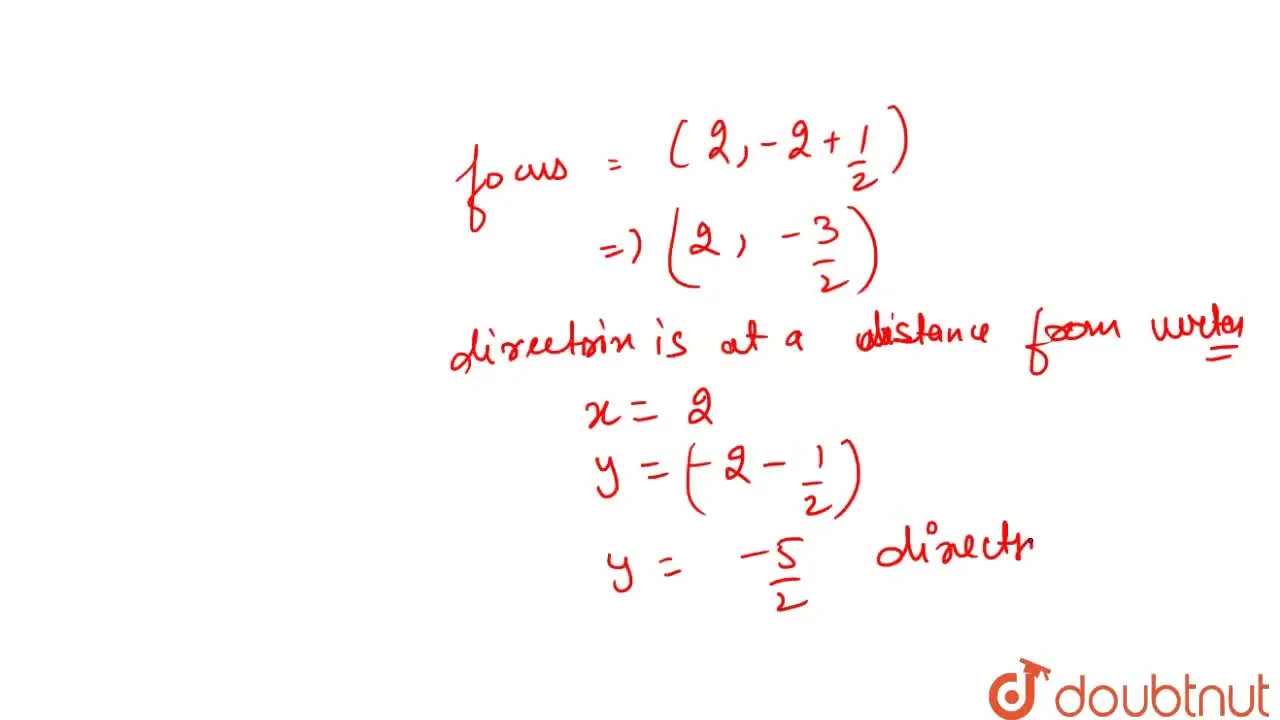Find the vertex, focus and directrix of the parabola x2=2(2x+y).
The correct Answer is:Vertex≡(2,−2),Focus≡(2,−3/2),Directrix:y=−52
We have x2=2(2x+y)
∴ x2−4x+4=2(y+2)
⇒ (x−2)2=2(y+2)
Comparing with (x−h)2=2(y−k), we get
Vertex of the parabola is (2,-2).
Length of latus rectum =4a=2
Axis of the parabola is x=2.
Also, parabola is concave upward.
Focus lies at distance a units above the vertex on the axis.
So, focus is (2,−2+12)≡(2,−32).
Directrix is at distance a units below the vertex and perpendicular to the axis.
Therefore, directrix is y=−2−12ory=−52.
Related Playlists
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise 5.37videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise 5.413videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise 5.111videos
PARABOLA
- BOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)5videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Question Bank19videos
PERMUTATION AND COMBINATION
Similar Questions
Find the vertex, focus and directrix of the parabola
x2+4x+2y−7=0 .View SolutionFind the vertex, focus and directrix of the parabola 4y2+12x−12y+39=0.
View SolutionFocus and directrix of the parabola x2=−8ay are
View SolutionFind the focus and directrix of the parabola 3x2+12x+8y=0.
View SolutionFind the vertex and the directrix of the parabola y2−3x−2y+7=0
View SolutionFind the vertex, focus, latus-rectum axis and directrix of the parabola x2−y−2x=0.
View SolutionFind the vertex and focus of the given parabola x2+4y=0
View SolutionFind the vertex, axis, focus, directrix, latus rectum of the parabola y2−8y−x+19=0
View SolutionFind the vertex, focus, axis , latus rectum and directrix of the parabola
y2+4x+6y+17=0View SolutionFind vertex, focus, directrix and latus rectum of the parabola y2+4x+4y−3=0.
View Solution