Find the values of p for which the equation x4−14x2+24x−3−p=0 has
(a) Two distinct negative real roots
(b) Two real roots of opposite sign
(c) Four distinct real roots
(d) No real roots
To examine the roots of the equation x4−14x2+24x−3−p=0 , let us first draw the graph of the function.
f(x)=x4−14x2+24x−3
f'(x)=4x3−28x+24
=4(x3−7x+6)
=4(x3−x2+x2−x−6x+6)
=4(x−1)(x2+x−6)
=4(x−1)(x+3)(x−2)
f'(x)=0∴x=1,2,−3
Also the leading coefficient is 1, when x→±∞,f(x)→∞.
Sign scheme of f'(x) is as follows.

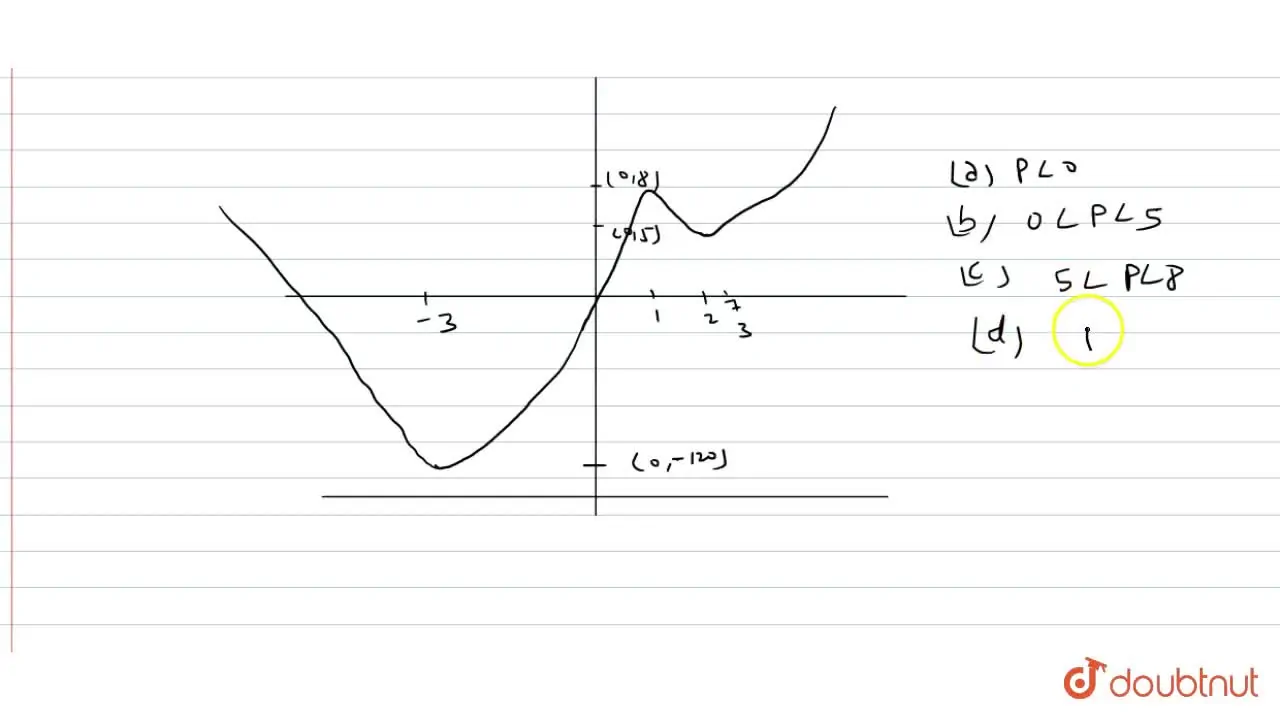
Clearly, from the sign scheme, x = -3 and x = 2 are the points of minima and x = 1 is the point of maxima.
f(1)=8,f(2)=5 and f(−3)=−120
Also f(0)=−3
So the graph of y=f(x) is as shown in the following figure.

Now to examine the roots of the equation x4−14x2+24x−3=p, we draw the straight line y = p and find the intersection of y=f(x) and y=p.
Now for two distinct negative real roots of f(x)=p,y=p must cu ty=f(x) between point C and the x-axis. Hence the values of 'p' for two negative roots are (-120,0).
For two real roots of opposite sign, y = p must cut y = f(x) between points H and D. Hence the values of 'p' for two real roots of opposite sign are (-3,5).
For four distinct real roots, y=p must cut y=f(x) four times between points H and F. Hence the values of 'p' are (5,8).
For no real roots, y=p must lie below point C. Hence the values of 'p' are (−∞,−120).
Related Playlists
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise13videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise22videos
GRAPHICAL TRANSFORMATIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
Similar Questions
Find the values of k for which the equation x2−4x+k=0 has distinct real roots.
View SolutionFind the value of K for which the quadratic equation kx2+2x+1=0,has real and distinct root.
View SolutionFind the value of p for which the quadratic equation x (x-4) +p 0 has real roots.
View SolutionSuppose a, b, c are real numbers, and each of the equations x2+2ax+b2=0 and x2+2bx+c2=0 has two distinct real roots. Then the equation x2+2cx+a2=0 has - (A) Two distinct positive real roots (B) Two equal roots (C) One positive and one negative root (D) No real roots
View SolutionThe value of p for which the quadratic equation 2px2+6x+5=0 has real and distinct roots is
View SolutionThe value of k for which the equation (k−2)x2+8x+k+4=0 has both roots real, distinct and negative, is
View SolutionFind the values of a for which all roots of the equation 3x4+4x3–12x2+a=0 are real and distinct.
View SolutionThe equation x4–2x2=a has 4 distinct real roots, then
View SolutionThe quadratic equation 2x2−√5x+1=0 has
(a) two distinct real roots (b) two equal real roots
(c) no real roots (d) more than 2 real rootsView SolutionThe real number k for which the equation 2x3+3x+k=0 has two distinct real roots in [0, 1]
View Solution