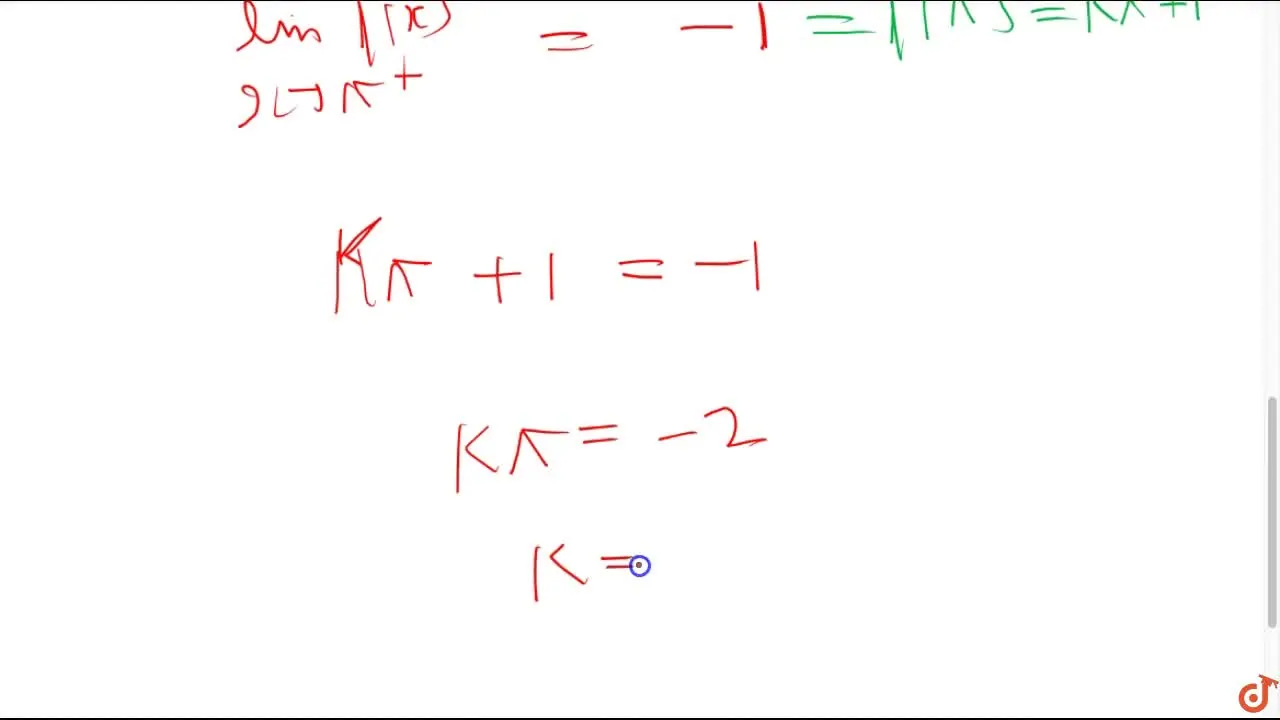Find the value of the constant so that the given function is continuous at the indicated point: at
Also
Since is continuous at
Related Playlists
Similar Questions
Find the value of the constant k so that the given function is continuous at the indicated point: f(x)={kx+1, if x≤πcosx, if x>π at x=π
View SolutionFind the value of the constant k so that the given function is continuous at the indicated point: f(x)={kx+1, if x≤53x−5, if x>5 at x=5
View SolutionFind the value of the constant k so that the given function is continuous at the indicated point: f(x)={k(x2+2), if x≤03x+1, if x>0 at x=0 .
View SolutionFind the value of the constant k so that the given function is continuous at the indicated point: f(x)={kx2, x≥14, x<1 at x=1
View SolutionFind the value of the constant k so that the given function is continuous at the indicated point: f(x)={k(x2−2x), if x<0cosx, if x≥0 at x=0
View SolutionFind the value of the constant k so that the given function is continuous at the indicated point: f(x)={1−cos2kxx2ifx≠08ifx=0 at x=0
View SolutionFind the value of the constant k so that the given function is continuous at the indicated point: f(x)={x2−25x−5, x≠5k, x=5 at x=5
View SolutionFind the value of the constant k so that the given function is continuous at the indicated point: f(x)={(x−1)tan(πx2) if x≠1k if x=1 at x=1
View SolutionFind the values of k so that the function f is continuous at the indicated point inf(x)={kx+1ifx≤πcosxifx>π at x=π
View SolutionFind the value of the constant k so that the given function is continuous at the indicated point: f(x)={x3+x2−16x+20(x−2)2, x≠2k, x=2 at x=0 .
View Solution