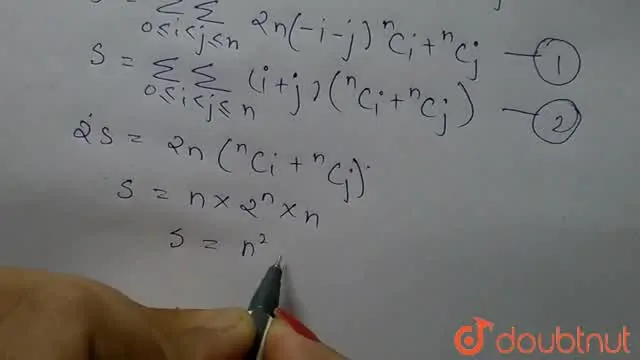
Find the value of (∑∑)0≤i<j≤n(1+j)(nCi+nCj).
Video Solution
Text Solution
Here sum does nto change if we replace i by n−1 and j by n−j.
By doing so, in fact we are writing the series in the reverse order.
Therefore, S=∑∑0≤i<j≤n(i+j)(.nCi+.nCj) (1)
=∑∑0≤i<j≤n(n−i+n−j)(.nCn−i+.nCn−j)
=∑∑0≤i<j≤n(2n(−i+j))(.nCi+.nCj) (2)
Adding (1) and (2), we have
2S=2n∑∑0≤i<j≤n(.nCi+.nCj)
or S=n×n2n=n22n
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Example10videos
BINOMIAL THEOREM
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Concept Application Exercise 8.117videos
BINOMIAL THEOREM
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Comprehension Type2videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE7videos
CIRCLE
Similar Questions
Find the value of ∑∑0≤i<j≤n(nCi+nCj).
View SolutionThe value of (∑∑)0≤i≤j≤n(nCi+nCj) is equal to
View SolutionFind the sum (∑∑)0≤i<j≤nnCi.
View SolutionFind the value of ∑∑0≤i≤j≤n(i+j)(nCi+nCj).
View SolutionFind the ∑∑0≤i<j≤n1.
View SolutionFind the sum ∑∑0≤i<j≤n nCinCj
View SolutionFind the value of ∑∑0≤i≤j≤ncnicnj.
View SolutionIf (1+x)n=C0=C1x+C2x2+…+Cnxn ,
find the values of the following
(∑∑)0≤i≤j≤n(i+j)(Ci±Cj)2View SolutionFind the sum ∑∑0≤i<j≤nnCi
View SolutionThe value of the expansion (∑∑)0≤i<j≤n(−1)i+j−1nCi⋅nCj=
View Solution