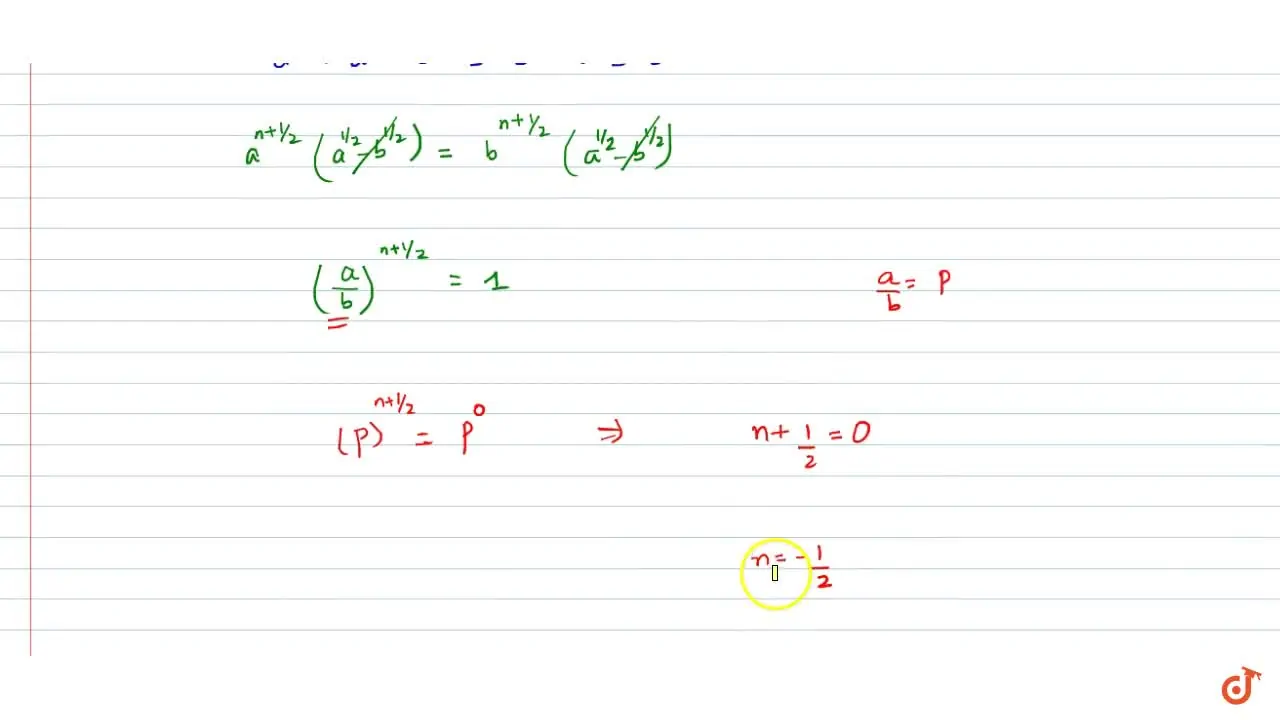Find the value of n so that an+1+bn+1an+bnmay be the geometric mean between a and b.
As given expession is geometric mean of a and b.
an+1+bn+1an+bn=(ab)12
⇒(an+1+bn+1)=an+12b12+bn+12a12
⇒an+1−an+12b12=bn+12a12−bn+1
⇒an+12(a12−b12)=bn+12(a12−b12)
⇒(ab)n+12=1
As a≠b,
∴n+12=0
n=−12
Related Playlists
- BOOK - NCERTCHAPTER - SEQUENCES AND SERIESEXERCISE - EXERCISE 9.114videos
SEQUENCES AND SERIES
- BOOK - NCERTCHAPTER - SEQUENCES AND SERIESEXERCISE - EXERCISE 9.56videos
SEQUENCES AND SERIES
- BOOK - NCERTCHAPTER - SEQUENCES AND SERIESEXERCISE - EXERCISE 9.218videos
SEQUENCES AND SERIES
- BOOK - NCERTCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 2.35videos
RELATIONS AND FUNCTIONS
- BOOK - NCERTCHAPTER - SETSEXERCISE - EXERCISE 1.57videos
SETS
Similar Questions
Find the value of n so that an+1+bn+1an+bn may be geometric mean between a and b.
View SolutionInsert n geometric means between a and b.
View SolutionWhat is the value of n so that an+1+bn+1an+bn is the geometric mean between a and b ? where a≠b
View SolutionFind the value of n so that an+2+bn+1an+bn may be the G.M. between a and b.
View SolutionFind n such that an+1+bn+1an+bn be the geometric mean of a and b.
View SolutionFind the value of n so that an+1+bn+1an+bnmay be the geometric mean between a and b.
View SolutionFind n such that an+1+bn+1an+bn be the arithmetic mean of a and b.
View SolutionFind n, so that an+1+bn+1an+bn(a≠b) be the HM between a and b.
View SolutionFind n, so that an+1+bn+1an+bn(a≠b) is the GM between a and b.
View SolutionFind n, so that an+1+bn+1an+bn(a≠b) be HM beween a and b.
View Solution