Find the total no. of orderd pairs (x,y) satisfying x(sin2x+1x2)=2sinxsin2y, where x∈(−π,0)∪(0,π)andy∈[0,2π] .
The correct Answer is:8
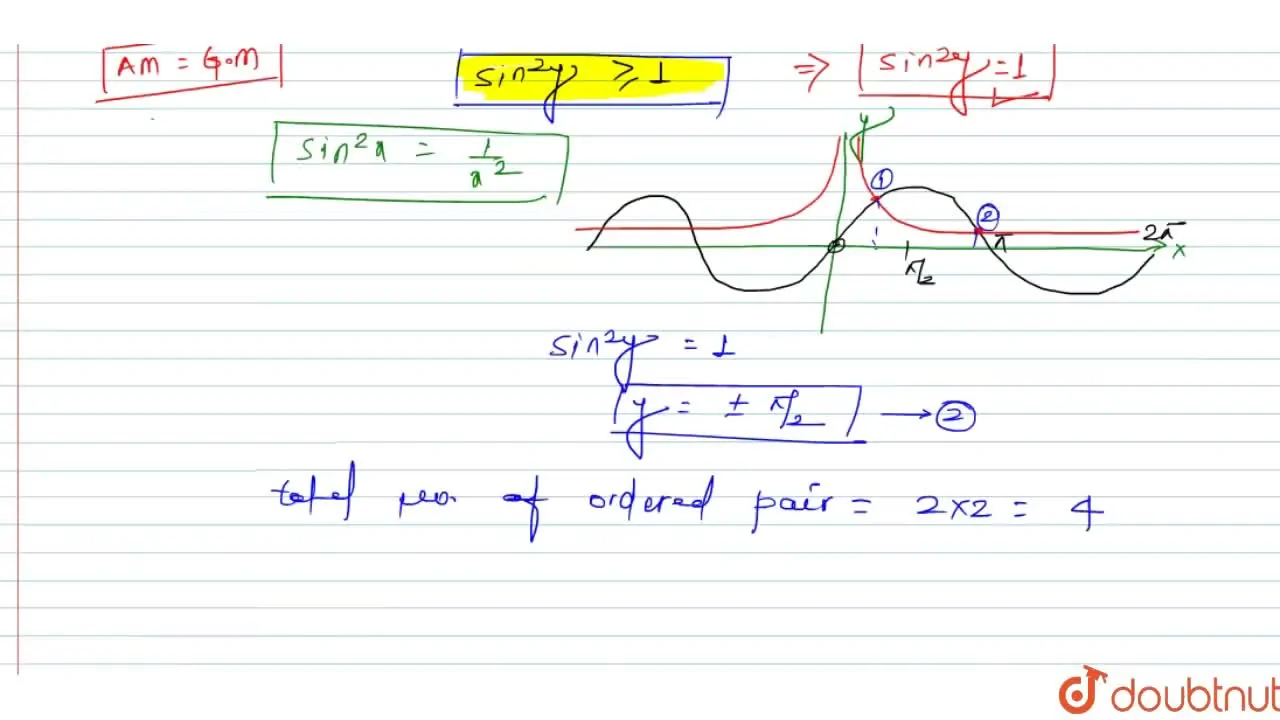
x(sin2x+1x2)=2sinxsin2y
⇒sin2x+1x2=2(sinxx)sin2y
⇒sin2x+1x2≤2(sinxx)
But using A.M.≥G.M., we have
sin2x+1x2≥2sinxx
⇒sin2x=1x2
or |sinx|=∣∣∣1x∣∣∣
Draw the graph of y=|sinx| and y=∣∣∣1x∣∣∣ as shown in the following figure.

From the figure, we get the four values of x.
sin2y=1 gives y=π2,3π2.
so, there will be 4×2=8 ordered pairs.
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives ((JEE MAIN) Single correct Answer type)2videos
TRIGONOMETRIC EQUATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives ((JEE ADVANSED) Single correct answer type)3videos
TRIGONOMETRIC EQUATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Exercises (Linked comprehension type)20videos
TRIGONOMETRIC EQUATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - ARCHIVES INTEGER TYPE1videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - SINGLE CORRECT ANSWER TYPE38videos
TRIGONOMETRIC FUNCTIONS
Similar Questions
The total number of ordered pairs (x, y) satisfying |y|=cosxandy=sin−1(sinx), where x∈[−2π,3π] is equal to :
View SolutionNumber of ordered pair (x,y) which satisfies the relation x4+18x2=sin2y⋅cos2y , where y∈[0,2π]
View SolutionIf x,y∈[0,2π] then find the total number of order pair (x,y) satisfying the equation sinx.cosy=1
View SolutionNumber of ordered pairs (a, x) satisfying the equation sec2(a+2)x+a2−1=0;−π<x<π is
View SolutionNumber of ordered pair (x,y) which satisfy the equation 2sinx=y2+2y+3 where x∈[0,2π],y∈R is
(1) 0
(2) 1
(3) 2
(4) infiniteView SolutionThe number of ordered pairs which satisfy the equation x2+2xsin(xy)+1=0 are (where y∈[0,2π] ) (a) 1 (b) 2 (c) 3 (d) 0
View SolutionIf x∈[0,6π],y∈[0,6π] then the number of ordered pair (x,y) which satisfy the equation sin−1sinx+cos−1cosy=3π2 are
View SolutionThe number of ordered pair (x, y) satisfying the equation sin2(x+y)+cos2(x−y)=1 which lie on the circle x2+y2=π2 is _________.
View SolutionThe number of ordered pair(s) (x,y) which satisfy y=tan−1tanx and 16(x2+y2)−48πx+16πy+31π2=0 is
View SolutionFind the number solution are ordered pair (x,y) of the equation2sec2x+2cosec2y=2cos2x(1−cos2y) in [0,2π]
View Solution