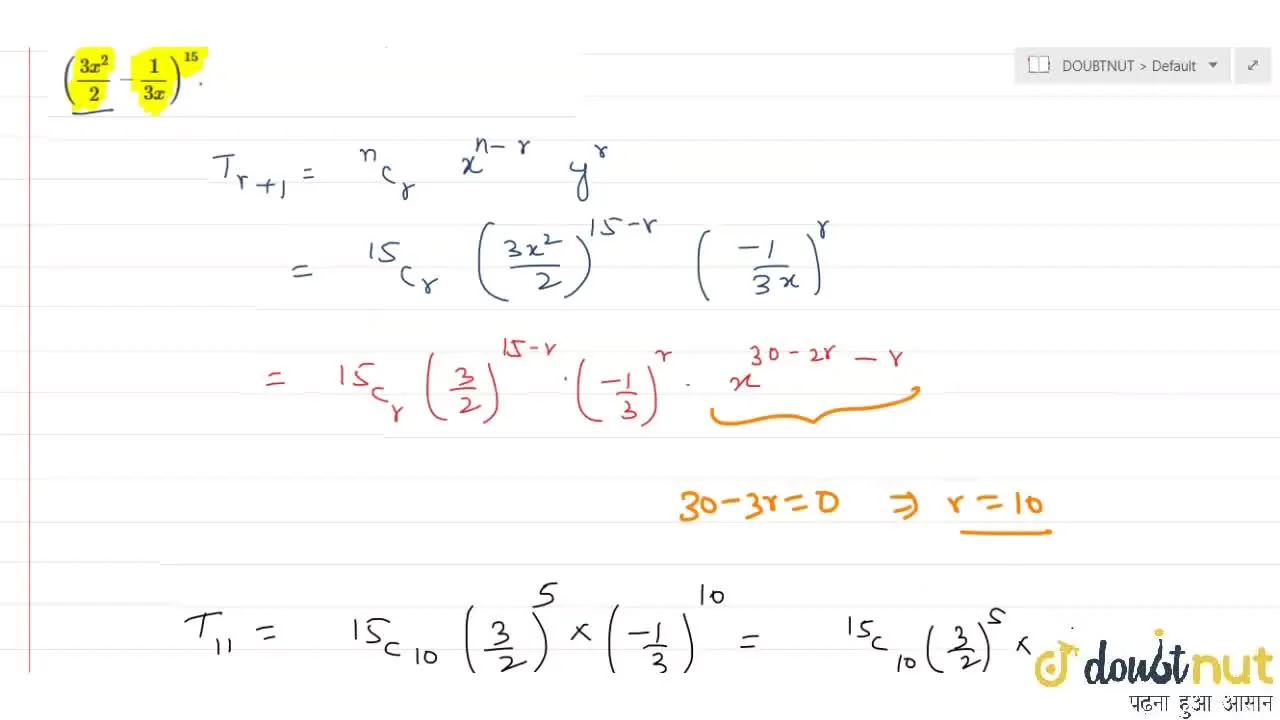Find the term independent of x, where x≠0, in the expansion of (3x22−13x)15.
Video Solution
Text Solution
Given expnsion is (3x22−13x)15 Let Tr+1 term is the general term.
Then, Tr+1=.15Cr(3x22)15−r(−13x)r
=.15Cr315−rx30−2r2r−15(−1)r.3−r.X−r
=.15Cr(−1)r315−2r2r−15x30−3r
For independent of x,
30−3r=0
3r=30⇒r=10
∴Tr+1=T10+1=1 th term is idependent of x.
∴T10+1=.15C10(−1)10315−20210−15
=.15C10(6)−5
=.15C10(16)5
|
Updated on:21/07/2023
Related Playlists
- BOOK - NCERT EXEMPLARCHAPTER - BINOMIAL THEOREMEXERCISE - Long Answer type question6videos
BINOMIAL THEOREM
- BOOK - NCERT EXEMPLARCHAPTER - BINOMIAL THEOREMEXERCISE - Objective type question16videos
BINOMIAL THEOREM
- BOOK - NCERT EXEMPLARCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - OBJECTIVE TYPE QUESTIONS16videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
Similar Questions
Find the term independent of 'x' , x≠0 in the expansion of (x2+3x)6
View SolutionFind the term independent of 'x' , x≠0 in the expansion of (3−x36)7
View SolutionFind the term independent of x in the
expansion of (32x2−13x)9View SolutionFind the term independent of x in the expansion of (32x2−13x)6 is-
View SolutionFind the terms independent of x in the expansion of (√x+13x2)10
View SolutionFind the term independent of x in the expansion of (32x2−13x)6.
View SolutionSimplify:- (1700 + 4100 + 5200) / ? = 55
View SolutionThe term independent of x in the expansion of (x3+2x2)15 is
View SolutionThe term independent of x in the expansion of (x3+2x2)15 is
View SolutionFind the term independent of x in the expansion of (1+x+2x3)[(3x2/2)−(1/3x)]9
View Solution