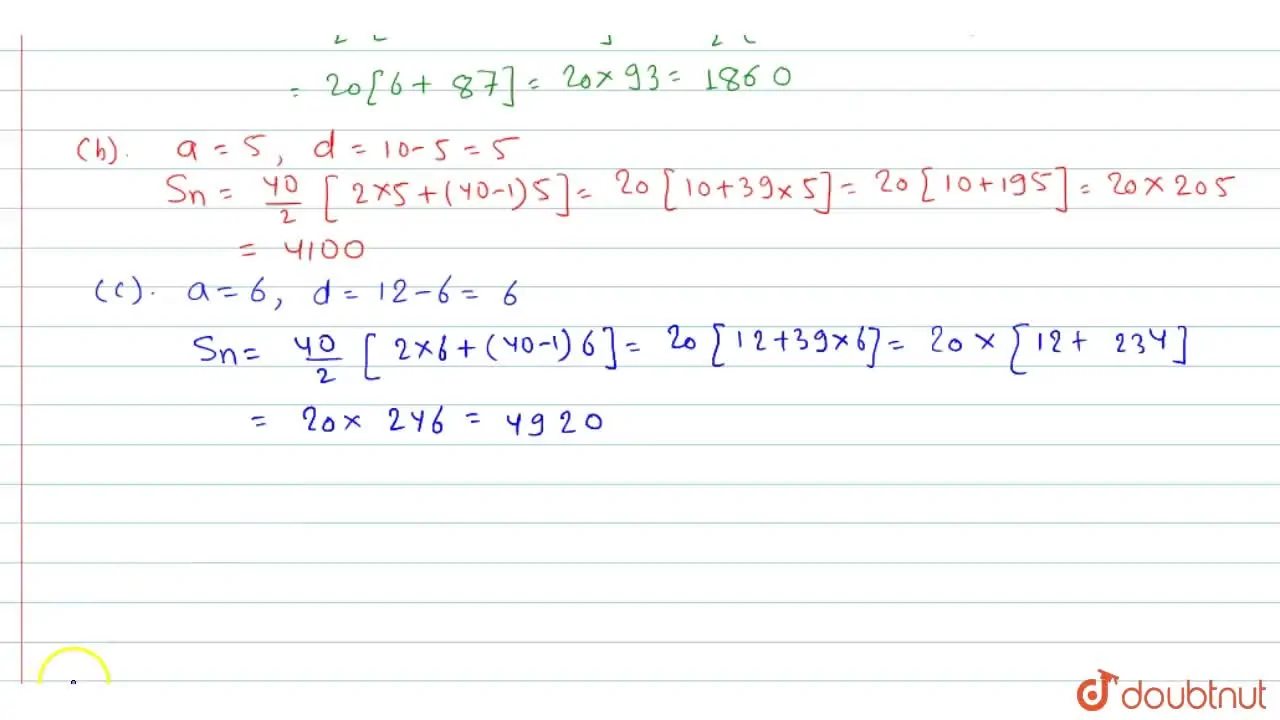Find the sum of the first 40 positive integers divisible by (a) 3 (b) 5 (c) 6.
Step by step video & image solution for Find the sum of the first 40 positive integers divisible by (a) 3 (b) 5 (c) 6. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Related Playlists
Similar Questions
Find the sum of the first 40 positive integers divisible by 6.
View SolutionThe difference of the squares of two consecutive odd integers is divisible by (a) 3 (b) 6 (c) 7 (d) 8
View SolutionFind the sum of first 100 even natural numbers which are divisible by 5.
View SolutionFind the sum of integers from 1 to 100 that are divisible by 2 or 5.
View SolutionFind the sum of all odd integers between 2 and 100 divisible by 3
View SolutionFind the sum of all odd integers between 2 and 100 divisible by 3
View SolutionFind the sum of :(i) the first 1000 positive integers(ii) the first n positive integers
View SolutionIf the product of n positive numbers is nn , then their sum is (a)a positive integer (b). divisible by n (c)equal to n+1/n (d)never less than n2
View SolutionIf the product of n positive numbers is nn , then their sum is (a) a positive integer (b) divisible by n (c) equal to n+1n (d) never less than n2
View SolutionThe sum of the integers from 1 to 100 which are not divisible by 3 or 5 is
View Solution