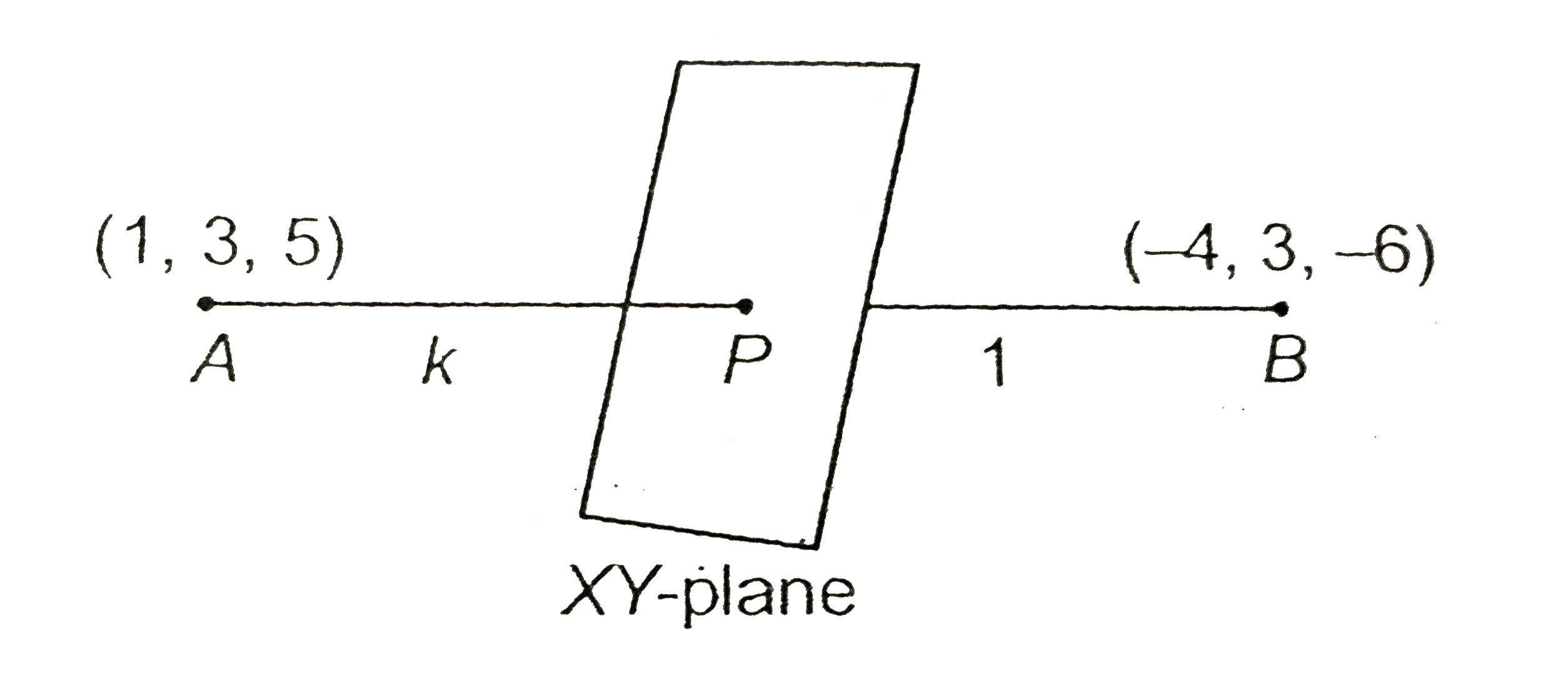
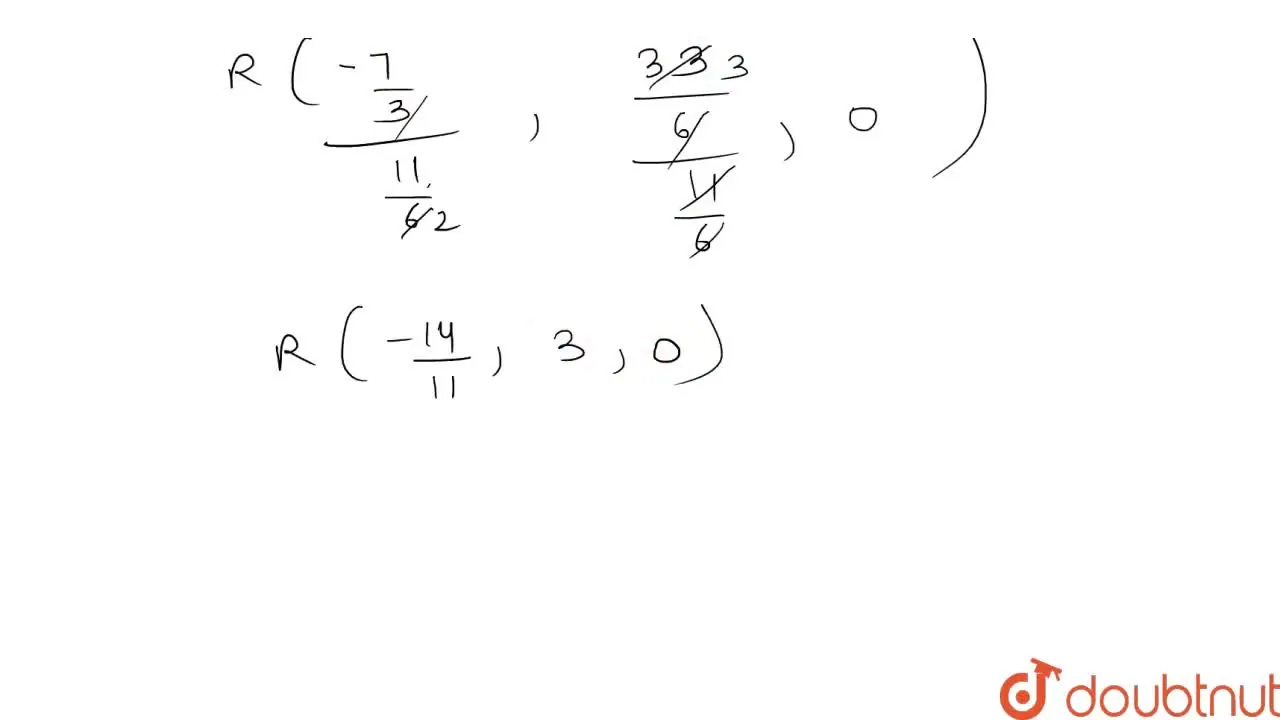Find the ratio in which the line segment joining the points (1, 3, 5) and (-4, 3, -6) is divided by
the XY-plane. Also, find the coordinates of the point of division.
Let the join of the line segment A(1, 3, 5) and B(-4, 3, -6) be divided by the XY-plane at a point
P in k : 1 Then the coordinates of P are given by
(−4k+1k+1,3k+3k+1,−6k+5k+1)...(i)
Now, P lies on XY-plane i.e. , z = 0
∴−6k+5k+1=0⇒k=56
So, the required ratio is 5 : 6
On putting k=56∈(i) we get the coordinates of P as (_1411,3,0).
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - Illustration4videos
THREE DIMENSIONAL GEOMETRY
- BOOK - AAKASH INSTITUTECHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - TRY YOURSELF97videos
THREE DIMENSIONAL GEOMETRY
- BOOK - AAKASH INSTITUTECHAPTER - STRAIGHT LINESEXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)5videos
STRAIGHT LINES
- BOOK - AAKASH INSTITUTECHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section - J (Akash Challengers Question)15videos
TRIGNOMETRIC FUNCTIONS
Similar Questions
Find the ratio in which the line joining the points (1, 3, 2), and (-2, 3, -4) is divided by the
YZ-plane. Also, find the coordinates of the point of division.View SolutionFind the ratio in which the line segment having the end points A(−1,−3,4) and B(4,2,−1) is divided by the xz−plane. Also, find the coordinates of the point of division.
View SolutionFind the ratio in which the line segment joining the points (3,5,7) and (-2,4,6) is divided by YZ plane
View SolutionFind the ratio in which the line segment joining the points (4,8,10) and (6,10,−8) is divided by the YZ -plane.
View SolutionFind the ratio in which the line segment joining the points (−3,10)and(6,−8) is divided by (−1,6).
View SolutionFind the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by (-1, 6).
View SolutionFind the ratio in which the line segment joining the points (2,4,5) and (3,-5,4) is divide by the yz-plane.
View SolutionIn which ratio the line segment joining the points
(2, 4, 5) and (3, -4, -5) is divided by the XY-plane?View SolutionFind the ratio in which the line segment joining the points (-1,7)and(4,-3) is divided by the poin(1,3).
View SolutionFind the ratio in which the line segment joining the points (2,-1,3) and (-1,2,1) is divided by the plane x+y+z=5.
View Solution