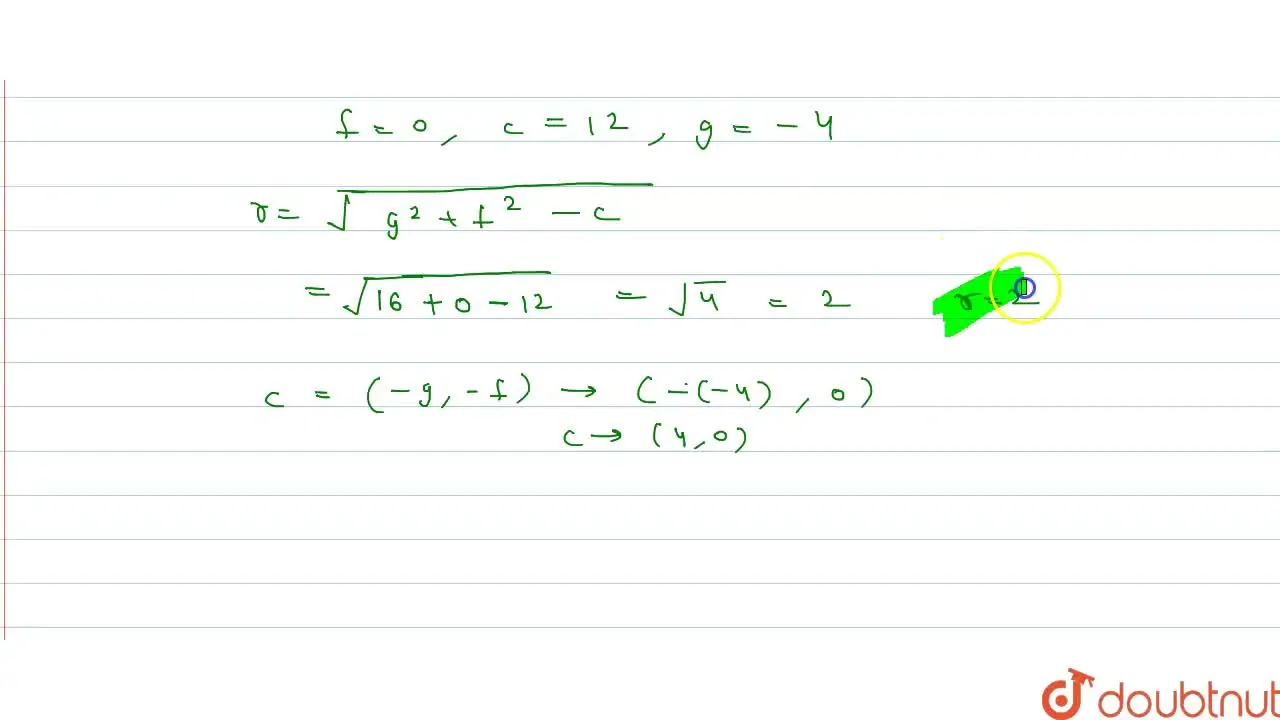Find the radius and centre of the circle passing through the points and .
The general equation of the circle is given by
where radius and centre
To find the required radius and centre, we first need to find the equation of the circle passing through the three given points.
Since, the circle passes through the point (2, 0), (6, 0) and (4, 2) these points will satisfy equation (1)
i.e., ,
and
,
Equation (2) and (3) given g = -4 and c = 12
Putting these value in (4) we get : f = 0
Now, radius and centre of the given circle is given by and respectively.
i.e., radius = and centre = i.e., (4, 0)
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - CONIC SECTIONSEXERCISE - Try ypurself42videos
CONIC SECTIONS
- BOOK - AAKASH INSTITUTECHAPTER - CONIC SECTIONSEXERCISE - Assignment (SECTION - A)55videos
CONIC SECTIONS
- BOOK - AAKASH INSTITUTECHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - section-J (Aakash Challengers Qestions)16videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
- BOOK - AAKASH INSTITUTECHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - section - J6videos
CONTINUITY AND DIFFERENTIABILITY
Similar Questions
Find the co-ordinates of the centre of the circle passing through the points (0,0),(−2,1) and (−3,2). Also find its radius.
View SolutionFind the equation of the circle passing through three points (0, 2), (3, 0) and (3, 2)
View SolutionFind the equation of the circle passing through the points
(i) (0,0),(5,0)and(3,3)
(ii) (1,2),(3,−4)and(5,−6)
(iii) (20,3),(19,8)and(2,−9)
Also, find the centre and radius in each case.View SolutionFind the centre and radius of the circle passing through the points P (-7,4) ,Q(0,3) and R (-4,5)
View SolutionUse distance formula to show that (3,3) is the centre of the circle passing through points (6,2),(0,4)and(4,6) . Find the radius of the circle
View SolutionWrite the coordinates of the centre of the circle passing through (0,0), (4,0) and (0,-6).
View SolutionStatement-1: The centre of the circle passing through the points (0, 0), (1, 0) and touching the circle C:x2+y2=9 lies inside the circle.
Statement-2: If a circle C1 passes through the centre of the circle C2 and also touches the circle, the radius of the circle C2 is twice the radius of circle C1View SolutionFind the equation of a circle passing through the points (5,7),(6,6)and(2,−2). Find its centre and radius.
View SolutionThe centre of a circle passing through the points (0, 0), (1, 0) and touching the circle x2+y2=9, is
View SolutionFind the equation of a circle passing through the points (5,7), (6,6) and (2,-1). Also, find its centre and radius.
View Solution