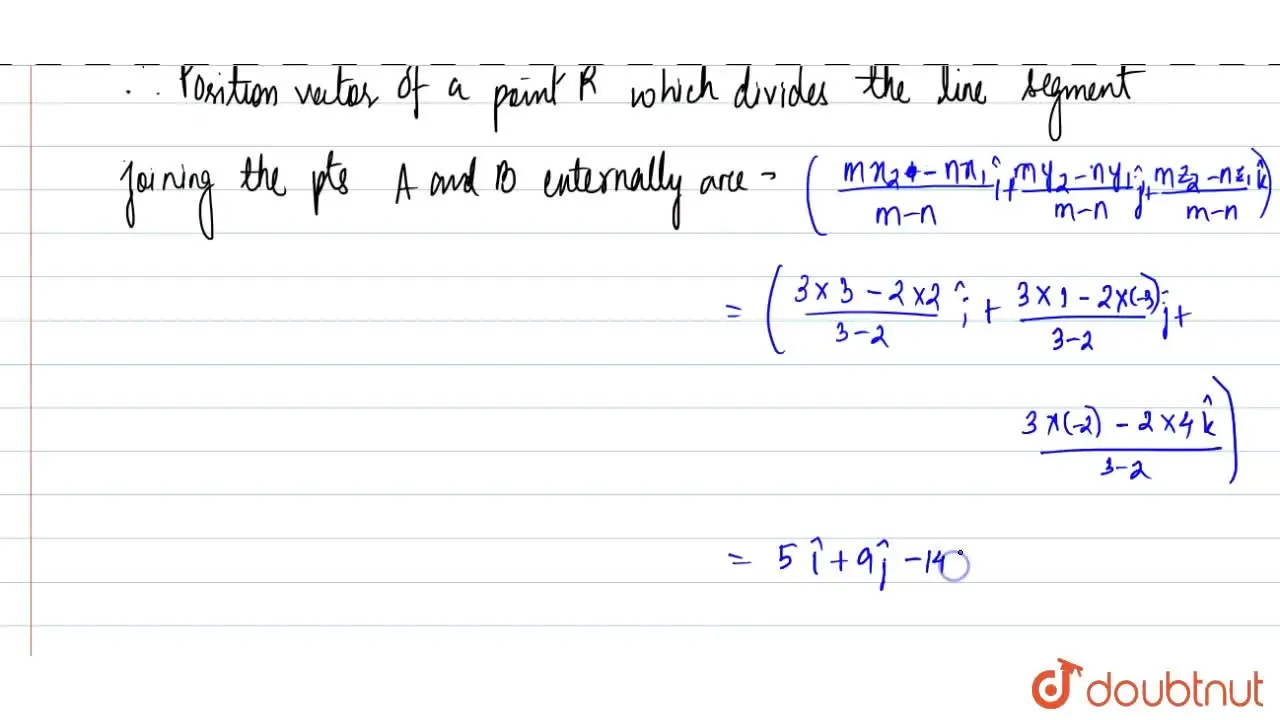Find the position vector of a point R which divides the line segment joining the points A(2,−3,4) and B(3,1,−2) externally in the ratio 3:2.
The position of A is (2ˆi−3ˆj+4ˆk).
The position vector of B is (3ˆi+ˆj−2ˆk).
Let R divide AB extenally in the ratio 3:2 .
Then, position vector of R.
=(3→b−2→a3−2)=3(3ˆi+ˆj−2ˆk)−2(2ˆi−3ˆj+4ˆk)1
=(5ˆi+9ˆj−14ˆk).
Hence, the position vector of R is (5ˆi+9ˆj−14ˆk).
Related Playlists
Similar Questions
Find the position vector of a point R which divides the line segment joining the points A(2,−3,4) and B(3,1,−2) externally in the ratio 3:2.
View SolutionFind the corrdinates of the point which divides the line segment joining the points A(2,-6,8) and B (-1,3,-4) externally in the ratio 1:3.
View SolutionFind the coordinates of the points R which divides the line segment joining the point P(2,−2,−4)andQ(3,−2,5) externally in the ratio 3:2.
View SolutionIf the point C divides the line segment joining the points A(2,−1,−4)andB(3,−2,5) externally in the ratio 3:2, then points C is
View SolutionThe co-ordinates of the points which divides line segment joining the point A(2,3,−1)andB(3,1,4) internally in the ratio 2:3 are
View SolutionThe point which divides the line segment joining the points A(0, 5) and B(5, 0) internally in the ratio 2:3 is __________
View SolutionFind the co-ordinates of a point which divides the line segment joining the points (1, -3) and (2, -2) in the ratio 3 : 2 externally.
View SolutionFind the coordinates of the point which divides the line segment joining the points (5,−2)and(9,6) internally and externally in the ration 3 : 1
View SolutionEvaluate the coordinates of the point which divides the line segment joining the points (8, -9) and (2, 3) internally in the ratio 1: 2.
View SolutionThe point which divides the line segment joining the points (7,-6) and (3,4) in ratio 1:2 internally lies in the
View Solution