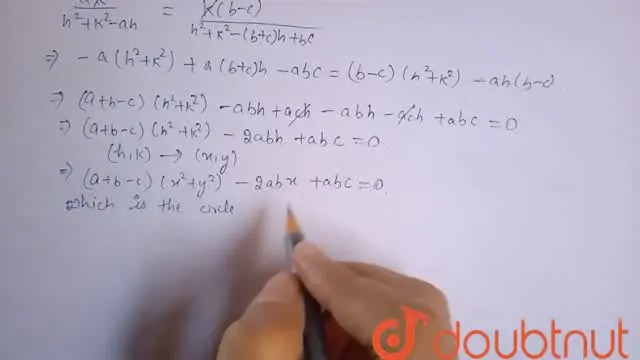
Find the locus of the point at which two given portions of the straight line subtend equal angle.
Step by step video & image solution for Find the locus of the point at which two given portions of the straight line subtend equal angle. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
Similar Questions
The locus of the point at which two given unequal circles subtend equal angles is: (A) a straight line(B) a circle (C) a parabola (D) an ellipse
View SolutionA line of fixed length a+b moves so that its ends are always on two fixed perpendicular straight lines. Then the locus of the point which divides this line into portions of length aandb is (a) an ellipse (b) parabola (c) straight line (d) none of these
View SolutionFind the locus of a point P If the join of the points (2,3) and (-1,5) subtends a right angle at P.
View SolutionFind the locus of the midpoint of the chords of the circle x2+y2=a2 which subtend a right angle at the point (c,0).
View SolutionFind the locus of the midpoint of the chords of the circle x2+y2=a2 which subtend a right angle at the point (0,0).
View SolutionThe locus of a point from which the two tangents to the ellipse are inclined at an angle α.
View SolutionFind the locus of the middle points of the chords of the parabola y2=4ax which subtend a right angle at the vertex of the parabola.
View SolutionFind the locus of the middle points of the chords of the parabola y2=4ax which subtend a right angle at the vertex of the parabola.
View SolutionFind the locus of the middle points of the chords of the parabola y2=4ax which subtend a right angle at the vertex of the parabola.
View SolutionFind the locus of a point, so that the join of points (-5, 1) and (3, 2) subtends a right angle at the moving point.
View Solution