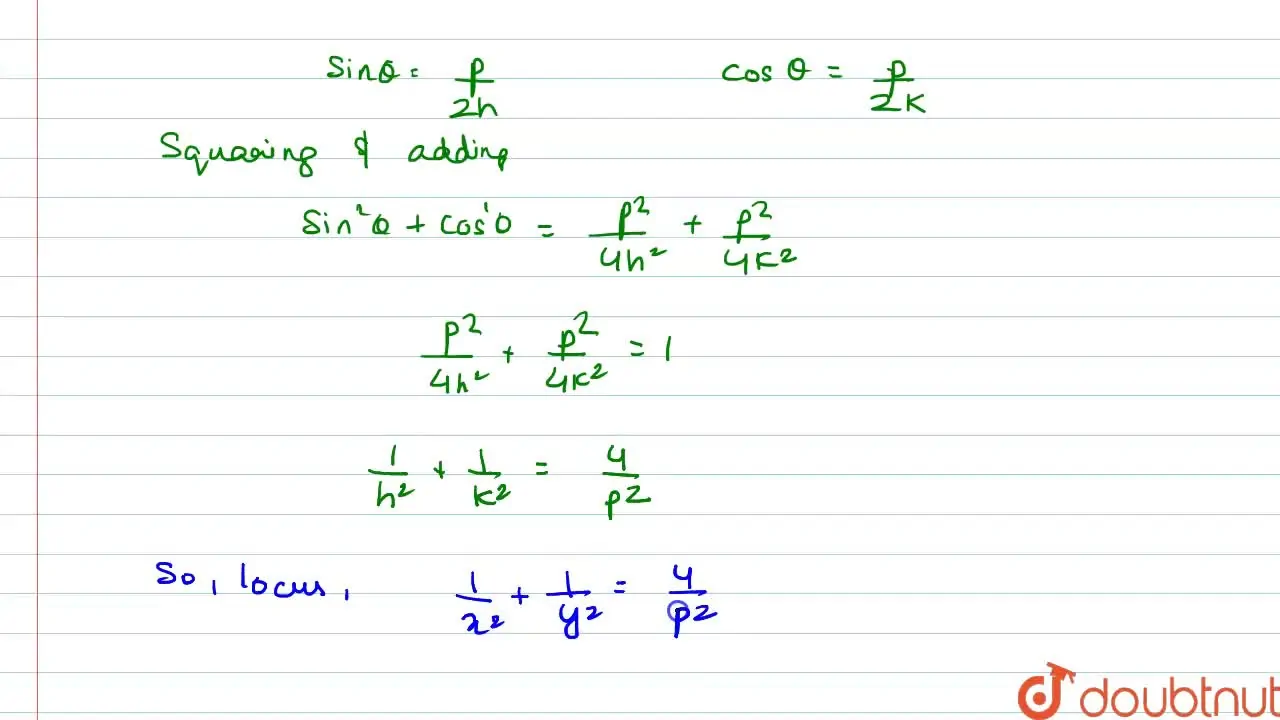Find the locus of the mid-point of the portion of the line xcosα+ysinα=p which is intercepted between the axes.
The correct Answer is:N/a
Given equation of the line is xsinθ+ycosθ=p
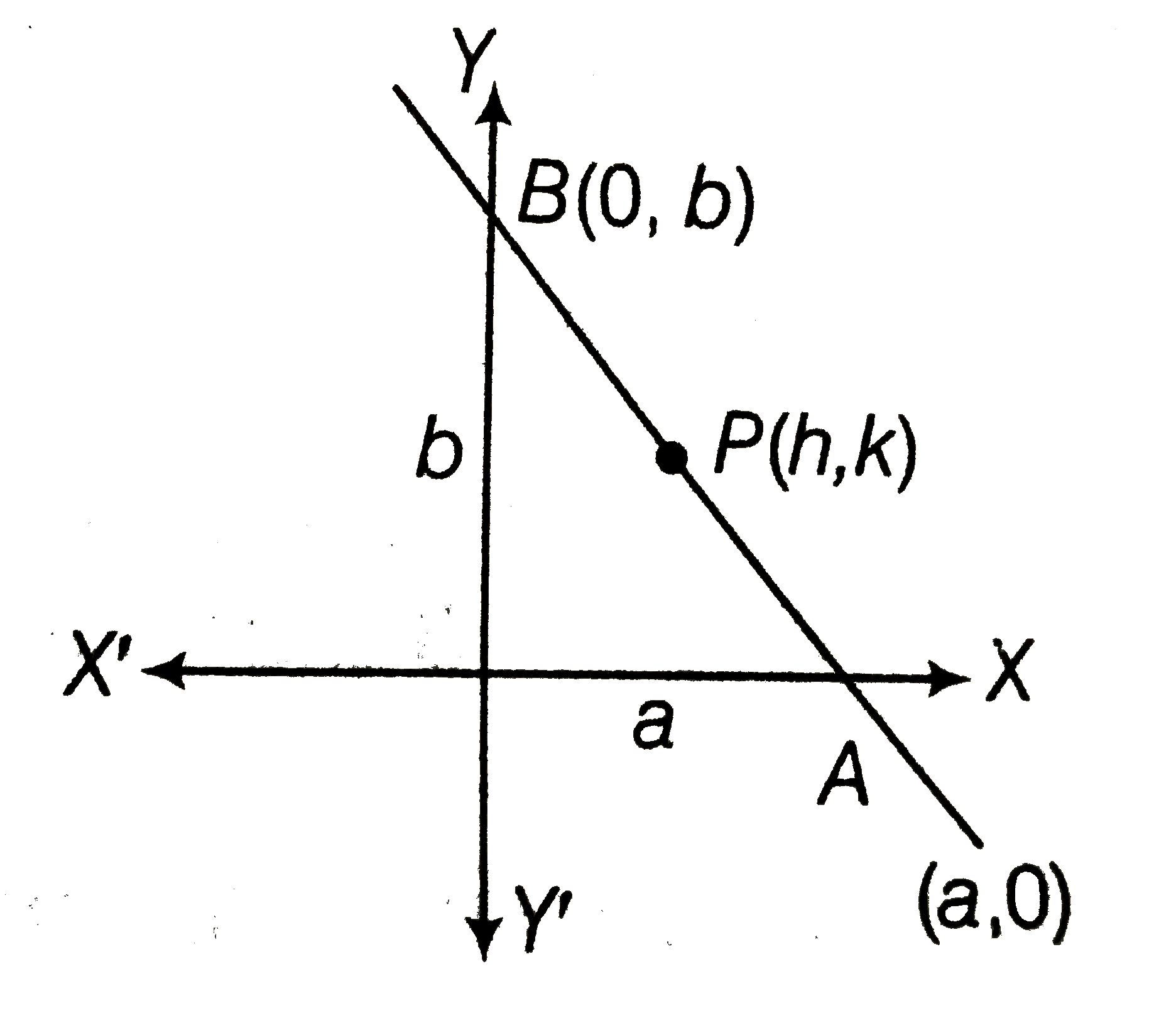
Let the mid-point of AB is p(h,k).
So, the mid-point of AB are (a2,b2)
Since, the point (a,0) lies on the line (i), then asinθ+0=p
⇒asinθ=p⇒a=psinθ
and the point (0,b) also lies on the line then, 0+bcosθ=p
⇒bcosθ=p⇒a=(p).(sinθ)
Now, mid-point of AB=(a2,a2) or (p2sinθ,p2cosθ)
∵p2sinθ=h⇒sinθ=p2h
⇒1=p24(1h2+1k2)
Locus of the mid-point is
4=p2(1x2+1y2)
⇒4x2y2=p2(x2+y2)
Related Playlists
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - TRUE/FALSE9videos
STRAIGHT LINES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - MATCHING THE COLUMN3videos
STRAIGHT LINES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Objective type questions20videos
STRAIGHT LINES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICSEXERCISE - FILLERS7videos
STATISTICS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - TRUE/FALSE9videos
TRIGONOMETRIC FUNCTIONS
Similar Questions
Find the locus of the middle point of the portion of the line xcosα+ysinα=p which is intercepted between the axes, given that p remains constant.
View SolutionFind the locus of the mid points of the portion of the lines xsinθ+ycosθ=p intercepted between the axes.
View SolutionFind the locues of the middle point of the portion of the line xcosα+ysinα=p, where p is a costant, intercepted between the axes.
View SolutionFind the locus of the midpoints of the portion of the normal to the parabola y2=4ax intercepted between the curve and the axis.
View SolutionFind the locus of the midpoints of the portion of the normal to the parabola y2=4ax intercepted between the curve and the axis.
View SolutionA line passes through the point (3,-2). Find the locus of the middle point of the portion the line intercepted between the axes.
View SolutionFind the equations of the straight lines which pass through the origin and trisect the portion of the straight line 2x+3y=6 which is intercepted between the axes.
View SolutionFind the equations of the straight lines which go through the origin and trisect the portion of the straight line 3x+y=12 which is intercepted between the axes of coordinates.
View SolutionFind the locus of the point of intersection of lines xcosα+ysinα=a and xsinα−ycosα=b(α is a variable).
View SolutionFind the locus of the point of intersection of lines xcosα+ysinα=a and xsinα−ycosα=b(α is a variable).
View Solution