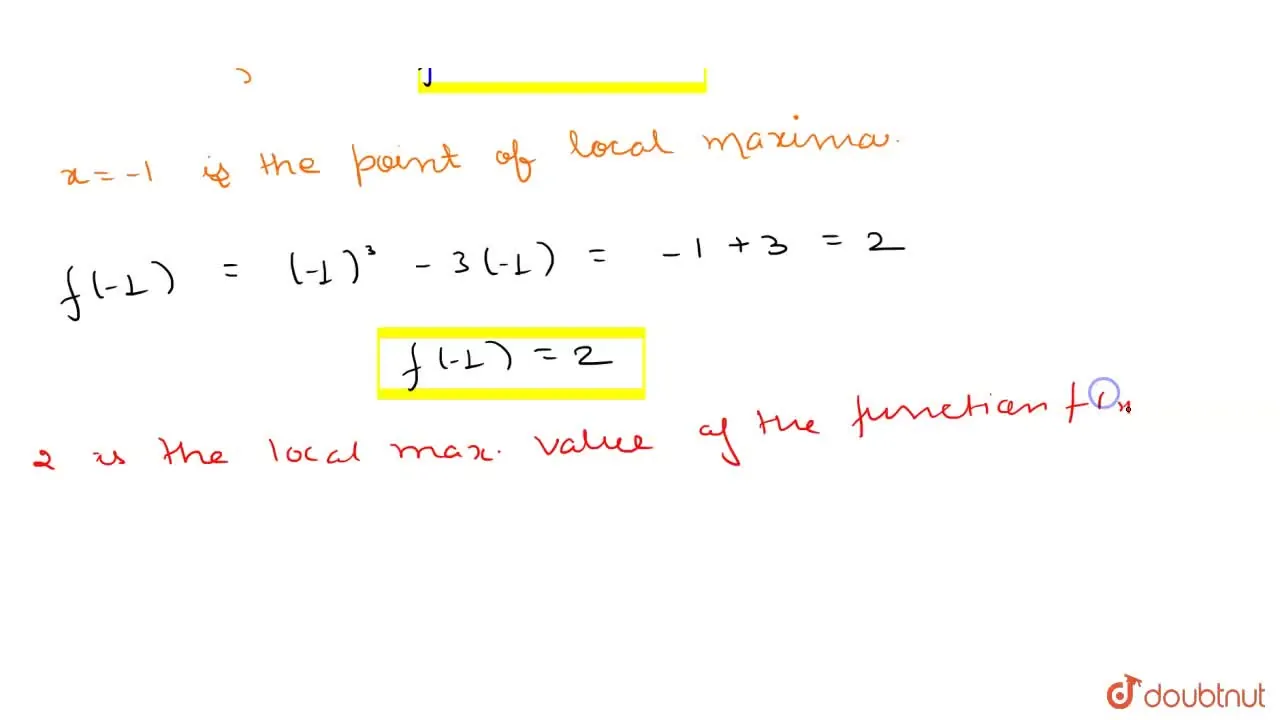Find the local maxima or local minima, if any, of
(i) f(x)=1(x2+2) (ii) f(x)=(x3−3x)
In each case, find the local maximum or the local minimum values, as the case may be
(i) f(x)=1(x2+2)⇒f'(x)=−2x(x2+2)2
For a local maxima or minima, we have f'(x)=0
∴f'(x)=0⇒−2x(x2_2)2=0⇒x=0
Now, when x is slightly less than 0, i.e., when x is negative, then f'(x)=−2x(x2+2)2 is positive.
When x is slightly greatern than 0 then f'(x)=−2x(x2+2)2<0
Thus, f'(x) changes sign from positive to negative.
So, x = 0 is a point of local maximum.
And, local maximum value is f(0)=1(02+2)=12
(ii) f(x)=(x3−3x)⇒f'(x)=(3x2−3)
Now, for a maximum or a minimum, we have f'(x)=0
Now, f'(x)=0⇒3x2−3=0
⇒3(x−1)(x+1)=0⇒x=1orx=−1
Thus, x=1andx=−1 are the candidates for local maxima or local minima.
Consider x=1
We know that f'(x)=3(x2−1)
When x is slightly less than 1 than x2 is slightly less than 1 and therefore, 3(x2−1) is positive.
Thus, f'(x) changes values from negative to positive as x increases through 1.
So, x = 1 is a point of local minimum.
Local minimum value =f(1)=(13−3×1)=−2
Consider x=−1
When x is slightly less than −1 then x2 is slightly more than 1.
So, 3(x2−1) is positive.
Again, when x is slightly more than −1 then x2 is slightly less than 1. So, 3(x2−1) is negative.
Thus, f'(x) changes sign from positive to negative as x increases through −1.
So, x=−1 is a point of local maximum.
Local maximum value =f(−1)=(−1)3−3×(−1)=2
Related Playlists
- BOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 11A21videos
APPLICATIONS OF DERIVATIVES
- BOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 11B17videos
APPLICATIONS OF DERIVATIVES
- BOOK - RS AGGARWALCHAPTER - ADJOINT AND INVERSE OF A MATRIXEXERCISE - Exercise 737videos
ADJOINT AND INVERSE OF A MATRIX
- BOOK - RS AGGARWALCHAPTER - AREA OF BOUNDED REGIONS EXERCISE - Exercise 1739videos
AREA OF BOUNDED REGIONS
Similar Questions
Find the local maximum and local minimum value of f(x)=x3−3x2−24x+5
View SolutionFind the local maxima or local minima of f(x)=x3−6x2+9x+15 Also, find the local maximum or local minimum values as the case may be
View SolutionFind the local maxima or local minima, if any, of the function f(x)=sinx+cosx, 0<x<π2 using the first derivative test.
View SolutionFind the points of local maxima or local minima, if any, of the following function, using the first derivative test. Also, find the local maximum or local minimum values, as the case may be: f(x)=(x−5)4
View SolutionFind the points of local maxima or local minima, if any, of the following function, using the first derivative test. Also, find the local maximum or local minimum values, as the case may be: f(x)=x3(2x−1)3
View SolutionFind the points of local maxima or local minima, if any, of the following function, using the first derivative test. Also, find the local maximum or local minimum values, as the case may be: f(x)=sin2x−x,−π2≤x≤π2
View SolutionFind the points of local maxima or local minima, if any, of the following function, using the first derivative test. Also, find the local maximum or local minimum values, as the case may be: f(x)=x2+2x,x>0
View SolutionFind the points of local maxima or local minima, if any, of the following function, using the first derivative test. Also, find the local maximum or local minimum values, as the case may be: f(x)=(x−1)(x+2)2
View SolutionFind the points of local maxima or local minima, if any, of the following function, using the first derivative test. Also, find the local maximum or local minimum values, as the case may be: f(x)=cosx ,0<x<π
View SolutionFind the local maxima and minima of the function f(x)=2x3−21x2+36x−20.
View Solution