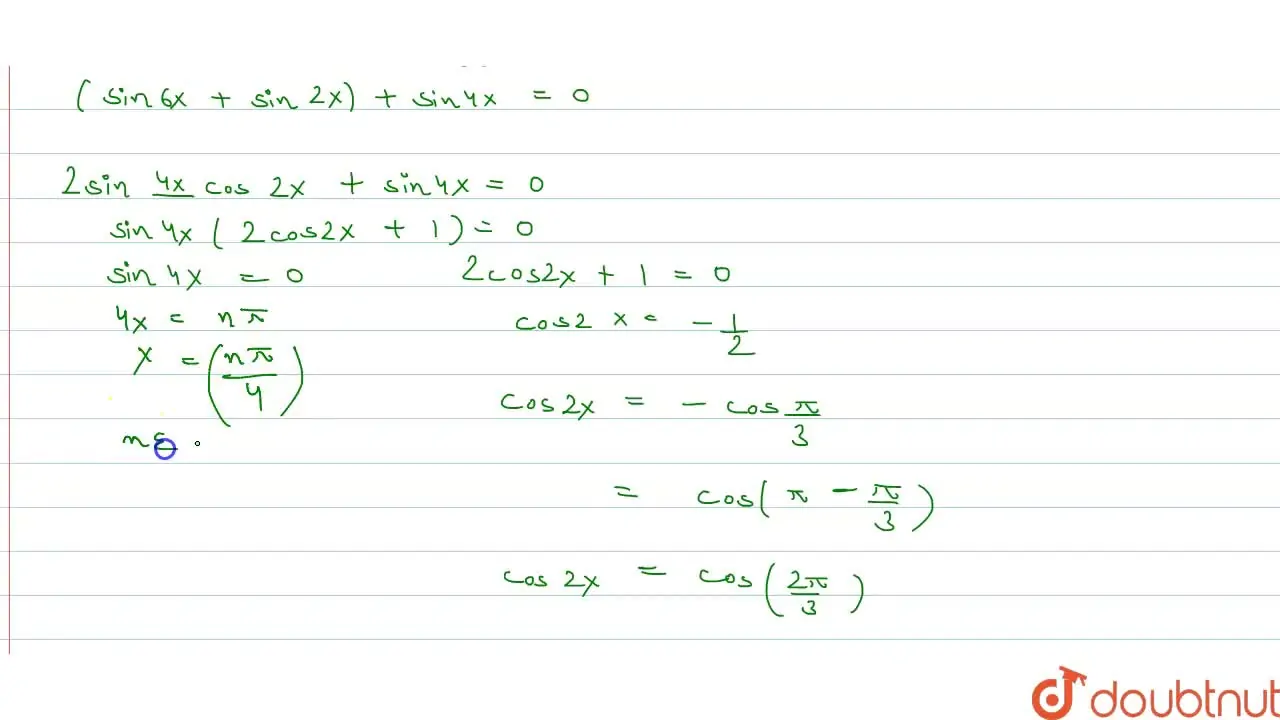Find the general solution of the equation sin2x+sin4x+sin6x=0.
sin2x+sin4x+sin6x=0.
∴(sin6x+sin2x)+sin4x=0
∴2sin(6x+2x2)cos(6x−2x2)+sin4x=0
∴2sin4xcos2x+sin4x=0
∴sin4x(2cos2x+1)=0
∴ either sin4x=0or2cos2x+1=0
∴ either sin4x=0or2cos2x=−1
∴ either sin4x=0orcos2x=−12
∴ either sin4x=0orcos2x=−cos.π3
∴ either sin4x=0orcos2x=cos(π−π3)......[∵cos(π−θ)=−cosθ]
∴either sin4x=0orcos2x=cos.2π3
The general solution of sinθ=0isθ=nπ,n∈Z and cosθ=cosα is θ=2nπ±α,n∈Z.
∴ the required general solution is given by
4x=nπ,n∈Zor2x=2nπ±α2π3,n∈Z
i.e., x=nπ4,n∈Zorx=nπ±π3,n∈Z.
Related Playlists
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Theory Questions1videos
TRIGONOMETRIC FUNCTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Examples for Practise44videos
TRIGONOMETRIC FUNCTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CHOICE QUESTIONS8videos
THREE DIMENSIONAL GEOMETRY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - VECTORSEXERCISE - Multiple choice question10videos
VECTORS
Similar Questions
Find the general solution of the equation sin x = tan x .
View SolutionThe general solution of the equation 2sinx+1=0 is:
View SolutionFind the general solution of the equation, sin3x+cos4x−4sin7x=cos10x+sin17x.
View SolutionIf x∈[0,π2] then the number of solutions of the equation sin 7x + sin 4x + sin x = 0 is
View SolutionFind the number of solutions of the equation sin5xcos3x=sin6xcos2x,x∈[0,π]
View SolutionFind the general solution of each of the equations :
(i) sin2x=−12
(ii) tan3x=−1View SolutionFind the general solution of the following equations
sin7x=sin3xView SolutionThe solution of the equation sin2x+sin4x=2sin3x is
View SolutionFind the general solutions of equation sin4x+cos4x=sinxcosx
View SolutionFind the general solution of sinx+sin5x=sin2x+sin4x.
View Solution