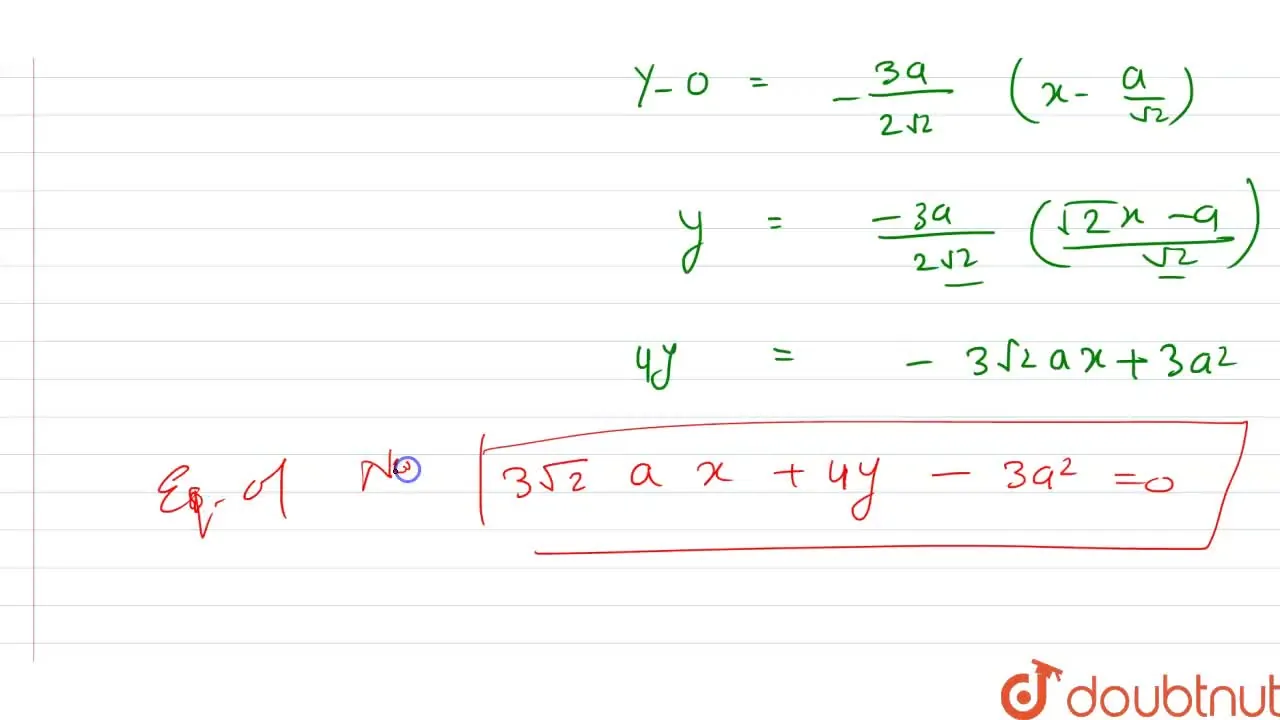Find the equations of the tangent and normal to the curve x=asin3t,y=cos2t at t=π4
We have
x=sin3t⇒dxdt=3cos3t
and y=cos2t⇒dydt=−2sin2t
∴dydx=(.dy/dt)(.dx/dt)=−2sin2t3cos3t
⇒[dydx]t=π4=−2sin(2×π4)3cos(3×π4)=−2sin(.π/2)−3cos(.π/4)=2√23
When t=π4, we have x=sin3π4=sin(π−π4)=sinπ4=1√2andy=cos2π4=cosπ2=0
∴ point of contact of P(1√2,0)
Equation of the tangent at the point P is given by
y−0x−1√2=2√23
⇒√2y√2x−1=2√23
⇒3√2y=4x−2√2
⇒2√2x−3y−2=0
Equation of the normal at the point P is given by
y−0x−1√2=−32√2⇒√2y√2x−1=−32√2
⇒4y=−3√2x+3⇒3√2x+4y−3=0
Related Playlists
- BOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 11A21videos
APPLICATIONS OF DERIVATIVES
- BOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 11B17videos
APPLICATIONS OF DERIVATIVES
- BOOK - RS AGGARWALCHAPTER - ADJOINT AND INVERSE OF A MATRIXEXERCISE - Exercise 737videos
ADJOINT AND INVERSE OF A MATRIX
- BOOK - RS AGGARWALCHAPTER - AREA OF BOUNDED REGIONS EXERCISE - Exercise 1739videos
AREA OF BOUNDED REGIONS
Similar Questions
Find the equations of the tangent and normal to the curve x=sin3t.,y=cos2t at t=π4
View SolutionFind the equation of the tangent at t=π4 to the curve : x=sin3t,y=cos2t.
View SolutionFind the equations of the tangent and the normal to the curve x=at2, y=2at at t=1 .
View SolutionThe slope of the tangent to the curve x=2 sin3t,y=3cos3t at t=π4 is
View SolutionFind the equations of the tangent and normal to the curve x=asin3θandy=acos3θ at θ=π4.
View SolutionFind the equations of tangent and normals to the curves y=sinx+cosx at x=π3
View SolutionFind the equation of the tangent to the curve x=sin3t , y=cos2t at t=π4 .
View SolutionFind the equations of the tangent and normal lines to the following curves :
y=sin2x at x=π2.View SolutionFind the equation of the tangent and the normal at the point 't, on the curve x=asin3t,y=bcos3t.
View SolutionFind the equations of the tangent and the normal to the curve xy=c2 at (ct, c/t) at the indicated points.
View Solution